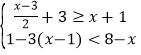Question

【题目】有一根40cm的金属棒,欲将其截成x根7cm的小段和y根9cm的小段,剩余部分作废料处理,若使废料最少,则正整数x,y应分别为 ( )

A. B. C. D.

Answer 1

【答案】C

【解析】分析：根据金属棒的长度是40cm即可得到关于x一元一次不等式，即7x+9y≤40，再根据x，y都是正整数，求得所有可能的结果，分别计算出废料的长度，再找出最少的费料对应的x、y值即可.

详解：根据题意得：7x+9y≤40，

则x≤.

∵40-9y≥0且y是正整数，

∴y的值可以是1或2或3或4，

当y=1时，x≤，则x=4，此时所剩的废料是：40-1×9-4×7=3（cm）；

当y=2时，x≤，则x=3，此时所剩的废料是：40-2×9-3×7=1（cm）；

当y=3时，x≤，则x=1，此时所剩的废料是：40-3×9-7=6（cm）；

当y=4时，x≤，则x=0（舍去）.

综上所述，当废料最少时，x=3，y=2.