Question

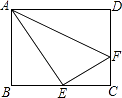
【题目】在数学拓展课上,小林发现折叠长方形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕为AF,点F在BC边上；②把△ADH翻折,点D落在AE边上的点G处,折痕为AH,点H在CD边上.若AD=6,AB=则∠HAF=___，GE=___.

Answer 1

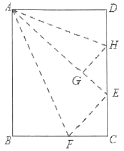
【答案】45°， 14-a

【解析】

由折叠的性质可得AB=AE=20-a，AD=AG=6，可求GE的长，再根据∠DAH=∠GAH，∠BAF=∠EAF，且∠DAH+∠GAH+∠BAF+∠EAF=90°，即可求出∠HAF的度数．

解：由折叠的性质可得：△ABF≌△AEF，△ADH≌△AGH
∴AB=AE=20-a，AD=AG=6，∠DAH=∠GAH，∠BAF=∠EAF
∴GE=AE-AG=20-a-6=14-a，
∵∠DAH+∠GAH+∠BAF+∠EAF=90°
∴2∠GAH+2∠EAF=90°
∴∠GAH+∠EAF=45°
∴∠HAF=45°
故答案为：45°，14-a，