题目内容
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.

(1) 60°;(2) 60°,证明见解析;(3)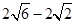 .
.
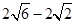 .
.试题分析:(1)由△ACP≌△BCQ得到∠APC=∠Q,根据圆周角定理,点P、E、C、Q 四点共圆,所以∠QEP=∠PCQ=6O°.
(2)同(1)可得.
(3)证明△GBC为等腰直角三角形,即可根据等腰直角三角形的性质求得BQ的长.
(1)60°.
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°.
又由题意可知,CP=CQ,∠PCQ=6O°,
∴∠ACP=∠BCQ.
∴△ACP≌△BCQ.
∴∠APC=∠Q.
∴点P、E、C、Q 四点共圆.
∴∠QEP=∠PCQ=6O°.
(2)60°.以∠DAC是锐角为例证明如下:
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°.
又由题意可知,CP=CQ,∠PCQ=6O°,
∴∠ACP=∠BCQ.
∴△ACP≌△BCQ.
∴∠APC=∠Q.
∴点P、E、C、Q 四点共圆.
∴∠QEP=∠PCQ=6O°.
(3)设PC与BQ交于点G,
由题意可求,∠APC=30°,∠PCB=45°.
又由(2)可证 ∠QEP=60°.
∴可证QE垂直平分PC,
∴△GBC为等腰直角三角形.
∵AC=4,
∴
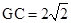 ,
,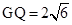
∴
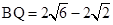 .
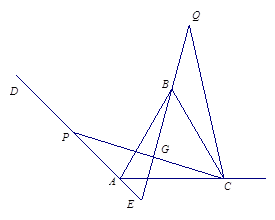
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 中,
中, ,
, ,
, .
.  的面积.(2分)
的面积.(2分) .(2分)
.(2分) 的坐标.(2分)
的坐标.(2分)
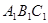 ,并写出
,并写出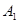 的坐标;
的坐标;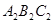 ,并写出
,并写出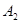 的坐标;
的坐标;