题目内容
【题目】如图,△ABC是边长为2的等边三角形,D是CA延长线上一点,以BD为边长作等边三角形BDE,连接AE.求:
①∠EAD的度数;
②求AE﹣AD的值.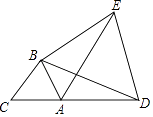
【答案】解:①∵△ABC和△BDE是等边三角形,
∴AB=BC=AC=2,BD=BE,∠ABC=∠C=∠BAC=∠DBE=60°,
∴∠ABC+∠ABD=∠DBE+∠ABD,
即∠CBD=∠ABE,
在△CBD和△ABE中,  ,
,
∴△CBD≌△ABE(SAS),
∴∠BAE=∠BCD=60°,
∴∠EAD=180°﹣60°﹣60°=60°;
②∵△CBD≌△ABE,
∴CD=AE,
∴AE﹣AD=CD﹣AD=AC=2
【解析】①由SAS证明△CBD≌△ABE,得出∠BAE=∠BCD=60°,即可得出∠EAD的度数;②由全等三角形的性质得出CD=AE,即可得出结果.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目