题目内容
【题目】如图，在四边形ABCD中，∠A=∠C=90°，BE平分∠B，DF平分∠D，求证：BE∥DF．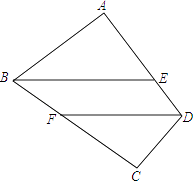 
【答案】证明：∵在四边形ABCD中，∠A=∠C=90°， ∴∠ABC+∠ADC=180°，
∵BE平分∠B，DF平分∠D，
∴∠EBF+∠FDC=90°，
∵∠C=90°，
∴∠DFC+∠FDC=90°，
∴∠EBF=∠DFC，
∴BE∥DF
【解析】根据角平分线的定义和四边形的内角和进行解答即可．
【考点精析】认真审题，首先需要了解平行线的判定(同位角相等，两直线平行;内错角相等，两直线平行;同旁内角互补，两直线平行)，还要掌握多边形内角与外角(多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°)的相关知识才是答题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
