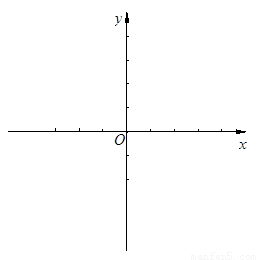题目内容
已知:抛物线y=a(x-t-1)2+t2(a,t是常数,a≠0,t≠0)的顶点是A,抛物线y=x2-2x+1的顶点是B.如图所示.(1)判断点A是否在抛物线y=x2-2x+1上,为什么?(2)如果抛物线y=a(x-t-1)2+t2经过点B,①求a的值;②这条抛物线与x轴的两个交点和它的顶点A能否构成直角三角形?③若能,求出t的值;若不能,请说明理由.

答案:
解析:
解析:
|
(1)答:点A在抛物线y=x2-2x+1上.(2)①a=-1.②当t=±1时,抛物线y=-(x-t-1)2+t2和x轴的两交点能与顶点A构成直角三角形.③略. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
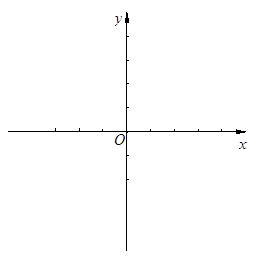
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左). ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由 个单位长度、每秒2
个单位长度、每秒2
 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).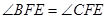 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由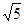 个单位长度、每秒2
个单位长度、每秒2
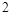 x交于点B、C(B在右、C在左).
x交于点B、C(B在右、C在左).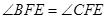 ,若存在,求出点F的坐标,若不存在,说明理由
,若存在,求出点F的坐标,若不存在,说明理由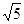 个单位长度、每秒2
个单位长度、每秒2