题目内容
【题目】（8分）某学校体育看台的侧面如图中阴影部分所示，看台有四级高度相等的小台阶，已知看台高为1.6米，现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和8C（杆子的底端分别为D、C），且∠DAB=66.5°（cos66.5°≈0.4）．
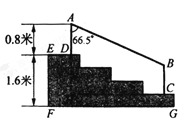
（1）求点D与点C的高度差DH；
（2）求所用不锈钢材料的总长度（即AD+AB+BC的长）．
【答案】（1）1.2；（2）4.6．
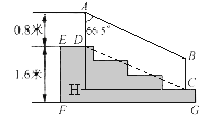
【解析】试题（1）已知看台有四个台阶组成，由图可看出DH由三个台阶组成，看台的总高度已知，则DH的长不难求得；
（2）连结CD，则四边形ABCD是平行四边形，从而得到CD=AB，再利用三角函数可求得CD，AB的长．那么所用不锈钢材料的总长度
就不难得到了．
试题解析：（1）DH=
EF=
=1.2（米），所以DH为1.2米；
（2）连结CD，∵
， ∴四边形ABCD是平行四边形，∴CD=AB，AB∥DC，∴∠CDH=∠BAD=66.5°，Rt△CDH中，
，
， ∴CD≈3，即AB≈3，∴
=AD+AB+BC≈0.8+3+0.8=4.6（米），即所用材料总长度约4.6米．
练习册系列答案
一线名师提优试卷系列答案
相关题目
