��Ŀ����
����Ŀ����A��B����������������ʾ�����ֱ�Ϊa��b����A��B�����ľ���ɼ�Ϊ|a��b|��
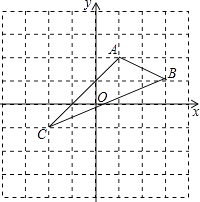
��1����ͼ����A��B����������������ʾ�����ֱ�Ϊ��2��4����A��B����ľ���Ϊ��![]()
��2����A,B����ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ�ͬʱ�������������˶������˶�ʱ��Ϊt�룬����������⣺
���˶�t���A������ʾ����Ϊ �� B������ʾ����Ϊ�����𰸾��ú�t�Ĵ���ʽ��ʾ��
�ڵ�tΪ��ֵʱ��A��B����ľ���Ϊ4��
���𰸡�
��1��6
��2��3t��2,4+t,�⣺��A��B����ľ���Ϊ4,�ࣻ3t��2����t+4����=4�������ã�2t��6=��4����ã�t=1��t=5����t=1��t=5ʱ,A��B����ľ���Ϊ4
���������⣺��1��AB=|4������2��|=|6|=6��
�ʴ�Ϊ��6��
��2���ٵ�A��ʾ����Ϊ��2+3��t=3t��2����B��ʾ����Ϊ4+1��t=4+4��
�ʴ�Ϊ��3t��2��4+t��
��1��ץס��֪����A��B�����ľ���ɼ�Ϊ|a��b|�����뼴����������
��2����ץס��֪����A��B������˶��ٶȺ�������A��B�����λ�ü�������˶�t���Ӻ�A��B��������ʾ�������ڸ���AB=4����������ֵ������⼴�ɡ�

��ϰ��ϵ�д�
 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
�����Ŀ