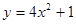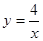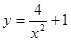题目内容
如图,在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.
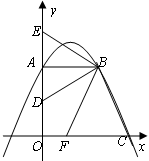
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ的周长最小,请直接写出P点的坐标.

(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ的周长最小,请直接写出P点的坐标.
(1)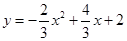 ;(2)
;(2)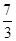 ;(3)(1,
;(3)(1,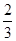 ).
).
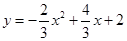 ;(2)
;(2)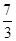 ;(3)(1,
;(3)(1,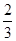 ).
).试题分析:(1)先根据题意得到点A、B、C的坐标,再根据待定系数法即可求得结果;
(2)先把(1)中的函数关系式配方为顶点式,即可求得顶点坐标,过G作GH⊥AB,垂足为H.即可得到AH=BH=1,GH=
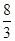 -2=
-2=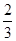 .由EA⊥AB,GH⊥AB,可得GH是△BEA的中位线,从而可得EA=3GH=
.由EA⊥AB,GH⊥AB,可得GH是△BEA的中位线,从而可得EA=3GH=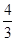 .过B作BM⊥OC,垂足为M.MB=OA=AB.由∠EBF=∠ABM=90°,可得∠EBA=∠FBM=90°-∠ABF.即可证得Rt△EBA≌Rt△FBM.再根据全等三角形的性质即可求得结果;
.过B作BM⊥OC,垂足为M.MB=OA=AB.由∠EBF=∠ABM=90°,可得∠EBA=∠FBM=90°-∠ABF.即可证得Rt△EBA≌Rt△FBM.再根据全等三角形的性质即可求得结果;(3)要使四边形BCPQ的周长最小,可将点C向上平移一个单位,再做关于对称轴对称的对称点C1,得点C1的坐标为(-1,1).可求出直线BC1的解析式为
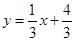 .再求的直线
.再求的直线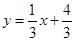 与对称轴x=1的交点即为点Q,坐标为(1,
与对称轴x=1的交点即为点Q,坐标为(1,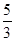 ).从而得到结果.
).从而得到结果.(1)由题意得A(0,2)、B(2,2)、C(3,0).
设经过A,B,C三点的抛物线的解析式为y=ax2+bx+2.
则
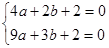 解得
解得 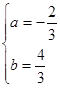
∴
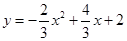 ;
;(2)由
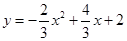 =
=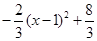 .
.∴顶点坐标为G(1,
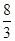 ).
).过G作GH⊥AB,垂足为H.
则AH=BH=1,GH=
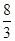 -2=
-2=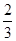 .
.∵EA⊥AB,GH⊥AB,
∴EA∥GH.
∴GH是△BEA的中位线 .
∴EA=3GH=
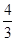 .
.过B作BM⊥OC,垂足为M .
则MB=OA=AB.
∵∠EBF=∠ABM=90°,
∴∠EBA=∠FBM=90°-∠ABF.
∴Rt△EBA≌Rt△FBM.
∴FM=EA=
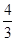 .
.∵CM=OC-OM=3-2=1,
∴CF=FM+CM=
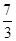 ;
;(3)要使四边形BCPQ的周长最小,可将点C向上平移一个单位,再做关于对称轴对称的对称点C1,得点C1的坐标为(-1,1).可求出直线BC1的解析式为
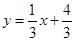 .
. 直线
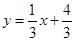 与对称轴x=1的交点即为点Q,坐标为(1,
与对称轴x=1的交点即为点Q,坐标为(1,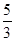 ).点P的坐标为(1,
).点P的坐标为(1,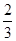 ).
).点评:二次函数的综合题是初中数学的重点和难点,在中考中极为常见,一般压轴题形式出现,难度较大.

练习册系列答案
相关题目
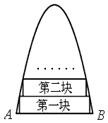
 的图象下列叙述正确的是( )
的图象下列叙述正确的是( ) =3
=3 有最大值2
有最大值2
 时,求直线AN的解析式.
时,求直线AN的解析式. 经过点
经过点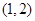 ,那么抛物线的解析式是_____________________。
,那么抛物线的解析式是_____________________。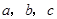 ,用
,用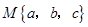 表示这三个数的平均数,用
表示这三个数的平均数,用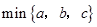 表示这三个数中最小的数.例如:
表示这三个数中最小的数.例如: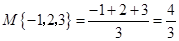 ;
;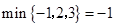 ;
;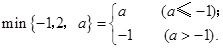
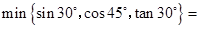 ;
;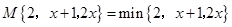 ,求
,求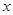 ;
; ,那么 (填
,那么 (填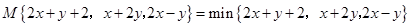 ,则
,则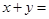 .
.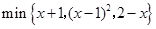 的最大值为 .
的最大值为 .