题目内容
已知⊙O1与⊙O2的半径分别为3cm与7cm，若⊙O1和⊙O2只有一个公共点，则两圆的圆心距为
- A.3cm
- B.4cm
- C.10cm
- D.4cm或10cm
D
分析：根据⊙O1和⊙O2只有一个公共点，则判断出两圆位置关系为内切或者外切，进行分类讨论两圆的圆心距．
解答：∵若⊙O1和⊙O2只有一个公共点，
∴两圆位置关系为内切或者外切，
当两圆外切时，d=3+7=10cm，
当两圆内切时，d=7-3=4cm，
故选D．
点评：本题主要考查圆与圆的位置关系的知识点，解答本题的关键是进行分类讨论，两圆有一个公共点，两圆内切或者外切，本题比较简单．
分析：根据⊙O1和⊙O2只有一个公共点，则判断出两圆位置关系为内切或者外切，进行分类讨论两圆的圆心距．
解答：∵若⊙O1和⊙O2只有一个公共点，
∴两圆位置关系为内切或者外切，
当两圆外切时，d=3+7=10cm，
当两圆内切时，d=7-3=4cm，
故选D．
点评：本题主要考查圆与圆的位置关系的知识点，解答本题的关键是进行分类讨论，两圆有一个公共点，两圆内切或者外切，本题比较简单．
练习册系列答案
相关题目
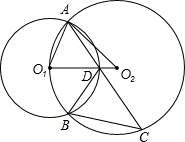如图，已知⊙O1与⊙O2的半径分别为r1，r2，⊙O2经过⊙O1的圆心O1，且两圆相交于A，B两点，C为⊙O2上的点，连接AC交⊙O1于D点，再连接BC，BD，AO1，AO2，O1O2，有如下四个结论：①∠BDC=∠AO1O2；②