题目内容
已知:如图,⊙O和⊙O’相交于A、B两点,AC是⊙O’的切线,交⊙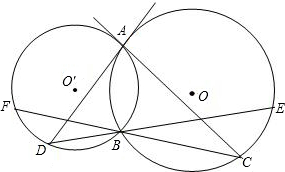 O于C点,连接CB并延长交⊙O’于点F,D为⊙O’上一点,且∠DAB=∠C,连接DB交延长交⊙O于点E.
O于C点,连接CB并延长交⊙O’于点F,D为⊙O’上一点,且∠DAB=∠C,连接DB交延长交⊙O于点E.①求证:DA是⊙O的切线;
②求证:AC2:AD2=BC:BD;
③若BF=4,CA=3
| 5 |
分析:(1)本题可过A作圆O的直径,然后证这条直径与AD垂直即可.可根据圆周角定理和已知的∠DAB=∠C来求解.
(2)本题的关键是证CF=DE,如图,如果证CF=DE,就必须证明O′Q=OP,就要证出∠OO′Q=∠O′OP,可通过证∠O′JR=∠OKR,即∠ABF=∠ABE来求解,证出CF=DE后,可根据切割线定理得出本题要求的结论.
(3)根据切割线定理和CA,FB的长,即可求出BC的长,也就能得出CF的长,(2)中已证得CF=DE,那么即可求出DE的长.
(2)本题的关键是证CF=DE,如图,如果证CF=DE,就必须证明O′Q=OP,就要证出∠OO′Q=∠O′OP,可通过证∠O′JR=∠OKR,即∠ABF=∠ABE来求解,证出CF=DE后,可根据切割线定理得出本题要求的结论.
(3)根据切割线定理和CA,FB的长,即可求出BC的长,也就能得出CF的长,(2)中已证得CF=DE,那么即可求出DE的长.
解答: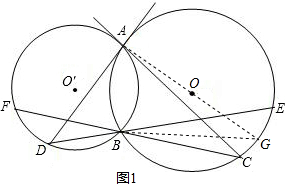 (1)证明:如图1,
(1)证明:如图1,
过A作⊙O的直径AG连接BG,则∠G=∠C,∠ABG=90°,
∵∠BAD=∠C,
∴∠BAD=∠G.
∵∠G+∠BAG=90°,
∴∠DAB+∠BAG=90°.
即∠DAG=90°.
∴AG⊥AD.
∴DA是圆O的切线.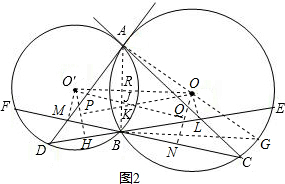
(2)证明:如图2:过O′作O′M⊥FC于M,作O′H⊥DE于H,
过O作ON⊥FC于N,过O作OL⊥DE于L;过O作OP⊥O′H于P,过O′作O′Q⊥ON于Q;
连接AB,OO′,则OO′⊥AB,OQ∥FC,OP∥DE,
∴∠ABF=∠O′JR,∠ABE=∠RKO.
∵∠ABF=∠BAC+∠C,∠ABE=∠D+∠DAB,
∵∠DAB=∠C,∠BAC=∠D,
∴∠ABF=∠ABE.
∴∠O′JR=∠OKR.
∴∠OO′Q=∠O′OP=90°-∠O′JR=90°-∠OKR.
∴OP=O′Q=OO′•cos∠OOP=OO•cos∠OOQ.
根据垂径定理易知:O′Q=
CF,OP=
DE,
∴CF=DE.
∵DA,AC分别是⊙O和⊙O′的切线,
∴CA2=CB•CF,DA2=DB•DE.
∴CA2:DA2=(CB:DB)•(CF:DE)=CB:DB.
(3)解:根据切割线定理可得:
∵CA2=CB•CF=CB•(CB+BF)=CB2+CB•BF,
∴45=CB2+4CB.
∴BC=4.
∴CF=BC+BF=9.
∴DE=CF=9.
 (1)证明:如图1,
(1)证明:如图1,过A作⊙O的直径AG连接BG,则∠G=∠C,∠ABG=90°,
∵∠BAD=∠C,
∴∠BAD=∠G.
∵∠G+∠BAG=90°,
∴∠DAB+∠BAG=90°.
即∠DAG=90°.
∴AG⊥AD.
∴DA是圆O的切线.

(2)证明:如图2:过O′作O′M⊥FC于M,作O′H⊥DE于H,
过O作ON⊥FC于N,过O作OL⊥DE于L;过O作OP⊥O′H于P,过O′作O′Q⊥ON于Q;
连接AB,OO′,则OO′⊥AB,OQ∥FC,OP∥DE,
∴∠ABF=∠O′JR,∠ABE=∠RKO.
∵∠ABF=∠BAC+∠C,∠ABE=∠D+∠DAB,
∵∠DAB=∠C,∠BAC=∠D,
∴∠ABF=∠ABE.
∴∠O′JR=∠OKR.
∴∠OO′Q=∠O′OP=90°-∠O′JR=90°-∠OKR.
∴OP=O′Q=OO′•cos∠OOP=OO•cos∠OOQ.
根据垂径定理易知:O′Q=
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=DE.
∵DA,AC分别是⊙O和⊙O′的切线,
∴CA2=CB•CF,DA2=DB•DE.
∴CA2:DA2=(CB:DB)•(CF:DE)=CB:DB.
(3)解:根据切割线定理可得:
∵CA2=CB•CF=CB•(CB+BF)=CB2+CB•BF,
∴45=CB2+4CB.
∴BC=4.
∴CF=BC+BF=9.
∴DE=CF=9.
点评:本题考查了切线的判定、圆周角定理、弦切角定理、切割线定理等知识点.本题中证得CF=DE是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
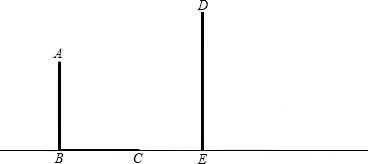 阳光下的投影长为6m,请你计算DE的长.
阳光下的投影长为6m,请你计算DE的长.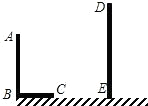 已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.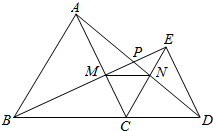 已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )
已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )