题目内容
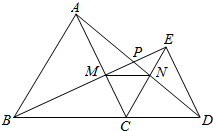 已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )
已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )| A、2个 | B、3个 | C、4个 | D、5个 |
分析:根据先证明△BCE≌△ACD,得出AD=BE,根据已知给出的条件即可得出答案;
解答:解:∵△ABC和△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴AD=BE,故选项①正确;
∵∠ACB=∠ACE=60°,由△BCE≌△ACD得:∠CBE=∠CAD,
∴∠BMC=∠ANC,故选项②正确;
由△BCE≌△ACD得:∠CBE=∠CAD,
∵∠ACB是△ACD的外角,
∴∠ACB=∠CAD+∠ADC=∠CBE+∠ADC=60°,
又∠APM是△PBD的外角,
∴∠APM=∠CBE+∠ADC=60°,故选项③正确;
在△ACN和△BCM中,
,
∴△ACN≌△BCM,
∴AN=BM,故选项④正确;
∴CM=CN,
∴△CMN为等腰三角形,∵∠MCN=60°,
∴△CMN是等边三角形,故选项⑤正确;
故选:D.
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴AD=BE,故选项①正确;
∵∠ACB=∠ACE=60°,由△BCE≌△ACD得:∠CBE=∠CAD,
∴∠BMC=∠ANC,故选项②正确;
由△BCE≌△ACD得:∠CBE=∠CAD,
∵∠ACB是△ACD的外角,
∴∠ACB=∠CAD+∠ADC=∠CBE+∠ADC=60°,
又∠APM是△PBD的外角,
∴∠APM=∠CBE+∠ADC=60°,故选项③正确;
在△ACN和△BCM中,
|
∴△ACN≌△BCM,
∴AN=BM,故选项④正确;
∴CM=CN,
∴△CMN为等腰三角形,∵∠MCN=60°,
∴△CMN是等边三角形,故选项⑤正确;
故选:D.
点评:本题考查了等边三角形及全等三角形的判定与性质,难度一般,关键是找出条件证明两个三角形全等.

练习册系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.