题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() (
(![]() 左
左![]() 右),交
右),交![]() 轴于点
轴于点![]() ,
,![]() ,且
,且![]() .
.
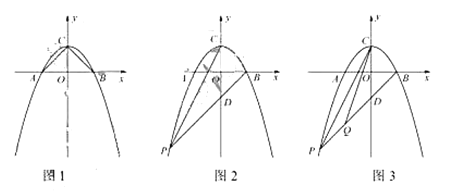
(1)如图,求![]() 、
、![]() 的值;
的值;
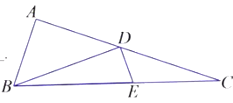
(2)如图,点![]() 在第三象限的抛物线上,
在第三象限的抛物线上,![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)如图,在(2)的条件下,点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,c=2(2)d=-t(t<-2);(3)
,c=2(2)d=-t(t<-2);(3) ![]()
【解析】
(1)根据三角形的面积公式求出B、C两点坐标,代入抛物线解析式,解方程组即可解决问题.
(2)设直线PB解析式为y=kx+b,把![]() ,B(2,0)代入,解方程组即可.
,B(2,0)代入,解方程组即可.
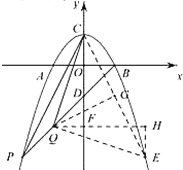
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 在抛物线上,连接
在抛物线上,连接![]() ,证明
,证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,
,![]() ,根据
,根据![]() ,得到
,得到![]() ,则
,则![]() 又
又![]() ,得到
,得到![]() ,则
,则![]() ,
,![]() ,即可求出
,即可求出![]() 的值,即可求解.
的值,即可求解.
(1)抛物线![]() 的对称轴为
的对称轴为![]() 轴,
轴,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
(2)![]() ,∵
,∵![]() ,∴直线
,∴直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() .
.
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,则
,则![]() 在抛物线上,连接
在抛物线上,连接![]() ,
,
则![]() ,
,![]() ,∴
,∴![]() ,
,
过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
设![]() ,则
,则![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目