题目内容
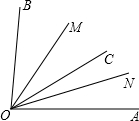如图，OM、ON分别是∠BOC和∠AOC的平分线，且∠AOB=84°．
（1）求∠MON的度数；
（2）当OC在∠AOB内转动时，∠MON的值是否会变？简单说明理由．
解：（1）∵OM、ON分别是∠BOC和∠AOC的平分线，
∴∠MOC=
∠BOC，∠CON=∠AOC，
∴∠MON=∠MOC+∠CON=∠BOC+∠AOC=（∠BOC+∠AOC）=∠AOB=×84°=42°；
（2）当OC在∠AOB内转动时，∠MON的值不变，
由（1）得到∠MON=∠AOB，
则只有∠AOB的大小不变，无论OC在∠AOB内怎样转动，∠MON的值都不会变．
分析：（1）由OM、ON分别是∠BOC和∠AOC的平分线，利用角平分线定义及等量代换即可得出所求角的度数；
（2）当OC在∠AOB内转动时，∠MON的值不发生变化，根据（1）的过程即可得到结果．
点评：此题考查了角平分线定义，熟练掌握角平分线定义是解本题的关键．
∴∠MOC=
∠BOC，∠CON=∠AOC，∴∠MON=∠MOC+∠CON=
∠BOC+∠AOC=（∠BOC+∠AOC）=∠AOB=×84°=42°；（2）当OC在∠AOB内转动时，∠MON的值不变，
由（1）得到∠MON=
∠AOB，则只有∠AOB的大小不变，无论OC在∠AOB内怎样转动，∠MON的值都不会变．
分析：（1）由OM、ON分别是∠BOC和∠AOC的平分线，利用角平分线定义及等量代换即可得出所求角的度数；
（2）当OC在∠AOB内转动时，∠MON的值不发生变化，根据（1）的过程即可得到结果．
点评：此题考查了角平分线定义，熟练掌握角平分线定义是解本题的关键．
练习册系列答案
相关题目
16、如图，OM⊥ON．已知正三角形ABC，两顶点A、B分别射线OM，ON上滑动，当∠OAB=21°时，∠NBC=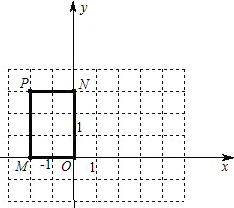
形PMON沿x轴正方向平移4个单位，得到矩形P′M′O′N′（P?P′，M?M′，O?O′，N?N′）
如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，直角∠MON的顶点O在AB上，OM、ON分别交CA、CB于点P、Q，∠MON绕点O任意旋转．当
如图，已知OM，ON分别平分∠AOC、∠BOC，若∠MON=45°，则OA⊥OB，你能说明为什么吗？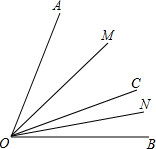
已知，OM和ON分别平分∠AOC和∠BOC．