题目内容
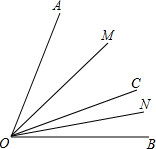 已知,OM和ON分别平分∠AOC和∠BOC.
已知,OM和ON分别平分∠AOC和∠BOC.(1)如图:若C为∠AOB内一点,探究∠MON与∠AOB的数量关系;
(2)若C为∠AOB外一点,且C不在OA、OB的反向延长线上,请你画出图形,并探究∠MON与∠AOB的数量关系.
分析:(1)根据角平分线的定义得到∠MOC=
∠AOC,∠NOC=
∠BOC,然后利用∠MOC+∠NOC=
∠AOC+
∠BOC即可得到∠MON=
∠AOB;
(2)分类讨论:直线OA和OB把平面分成四个部分,(1)中讨论了一个部分,然后再其他三个部分进行讨论:如图1,由于∠MOC=
∠AOC,∠NOC=
∠BOC,利用∠MOC-∠NOC=
∠AOC-
∠BOC即可得到∠MON=
∠AOB;如图2,由于∠MOC=
∠AOC,∠NOC=
∠BOC,利用∠NOC-∠MOC=
∠BOC-
∠AOC即可得到∠MON=
∠AOB;如图3,由于∠MOC=
∠AOC,∠NOC=
∠BOC,利用∠MOC+∠NOC=
∠AOC+
∠BOC=
(360°-∠AOB)即可得到∠MON=180°-
∠AOB.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)分类讨论:直线OA和OB把平面分成四个部分,(1)中讨论了一个部分,然后再其他三个部分进行讨论:如图1,由于∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: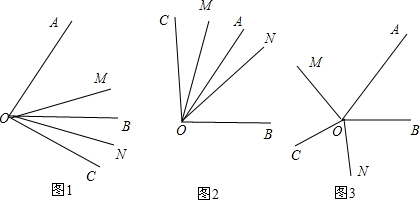 解:(1)∵OM和ON分别平分∠AOC和∠BOC,
解:(1)∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=
∠AOC,∠NOC=
∠BOC,
∴∠MOC+∠NOC=
∠AOC+
∠BOC=
∠AOB,
即∠MON=
∠AOB;
(2)如图1,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=
∠AOC,∠NOC=
∠BOC,
∴∠MOC-∠NOC=
∠AOC-
∠BOC=
∠AOB,
即∠MON=
∠AOB;
如图2,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=
∠AOC,∠NOC=
∠BOC,
∴∠NOC-∠MOC=
∠BOC-
∠AOC=
∠AOB,
即∠MON=
∠AOB;
如图3,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=
∠AOC,∠NOC=
∠BOC,
∴∠MOC+∠NOC=
∠AOC+
∠BOC=
(360°-∠AOB)
即∠MON=180°-
∠AOB.
 解:(1)∵OM和ON分别平分∠AOC和∠BOC,
解:(1)∵OM和ON分别平分∠AOC和∠BOC,∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MOC+∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠MON=
| 1 |
| 2 |
(2)如图1,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MOC-∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠MON=
| 1 |
| 2 |
如图2,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠NOC-∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠MON=
| 1 |
| 2 |
如图3,∵OM和ON分别平分∠AOC和∠BOC,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MOC+∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠MON=180°-
| 1 |
| 2 |
点评:本题考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

练习册系列答案
相关题目
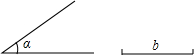 边的夹角等于∠α.(先填空,再根据步骤依次作出图形,保留作图痕迹)
边的夹角等于∠α.(先填空,再根据步骤依次作出图形,保留作图痕迹)
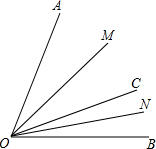 已知,OM和ON分别平分∠AOC和∠BOC.
已知,OM和ON分别平分∠AOC和∠BOC.