题目内容
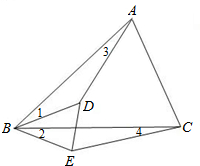 如图,D为△ABC内的一点,E为△ABC外的一点,且∠1=∠2,∠3=∠4.
如图,D为△ABC内的一点,E为△ABC外的一点,且∠1=∠2,∠3=∠4.(1)求证:△ABD∽△CBE.
(2)求证:△ABC∽△DBE.
分析:(1)观察图形,由已知的∠1=∠2,∠3=∠4,根据有两角对应相等的三角形相似,即可证得△ABD∽△CBE;
(2)根据已知的∠1=∠2,利用等式的性质,在∠1,∠2的两侧都加上∠DBC,即可得到∠ABC=∠DBE,同时再利用第一问已证的△ABD∽△CBE,根据相似三角形的对应边成比例得到:
=
,最后利用两边对应成比例,且夹角相等两三角形相似,即可证得△ABC∽△DBE.
(2)根据已知的∠1=∠2,利用等式的性质,在∠1,∠2的两侧都加上∠DBC,即可得到∠ABC=∠DBE,同时再利用第一问已证的△ABD∽△CBE,根据相似三角形的对应边成比例得到:
| AB |
| CB |
| BD |
| BE |
解答:证明:(1)∵∠1=∠2,∠3=∠4(已知),
∴△ABD∽△CBE(两角对应相等,两三角形相似);
(2)∵∠1=∠2,
∴∠1+∠DBC=∠2+∠DBC,
即∠ABC=∠DBE,
由(1)△ABD∽△CBE可得:
=
(相似三角形的对应边成比例),
∴△ABC∽△DBE(两边对应成比例,且夹角相等两三角形相似).
∴△ABD∽△CBE(两角对应相等,两三角形相似);
(2)∵∠1=∠2,
∴∠1+∠DBC=∠2+∠DBC,
即∠ABC=∠DBE,
由(1)△ABD∽△CBE可得:
| AB |
| CB |
| BD |
| BE |
∴△ABC∽△DBE(两边对应成比例,且夹角相等两三角形相似).
点评:此题考查了相似三角形的判定与性质,其中判定三角形相似的方法有:①如果两个三角形的三边对应成比例,那么这两个三角形相似;②如果两个三角形的两边对应成比例,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.相似三角形的性质主要有:两三角形相似,对应角相等,对应边成比例.解决本题时,一定要善于利用第一问已证的结论,运用已证的结论得到有关的知识为第二问的证明做准备.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
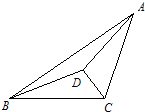 23、已知:如图,D为△ABC内一点,AC=BC,CD平分∠ACB.
23、已知:如图,D为△ABC内一点,AC=BC,CD平分∠ACB.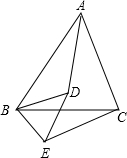 已知,如图,D为△ABC内一点连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD,BE、
已知,如图,D为△ABC内一点连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD,BE、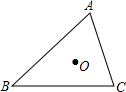 如图,O为△ABC内一点,以O为位似中心,作△A′B′C′∽△ABC,且相似比为2.
如图,O为△ABC内一点,以O为位似中心,作△A′B′C′∽△ABC,且相似比为2.