题目内容
(本小题满分10分)在图15-1至图15-3中,直线MN与线段AB相交于点O,∠1 = ∠2 = 45°.
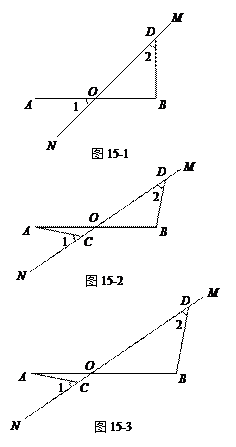
(1)如图15-1,若AO = OB,请写出AO与BD 的数量关系和位置关系;
(2)将图15-1中的MN绕点O顺时针旋转得到图15-2,其中AO = OB.
求证:AC = BD,AC ⊥ BD;
(3)将图15-2中的OB拉长为AO的k倍得到图15-3,求
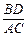 的值.
的值.
(1)AO = BD,AO⊥BD
(2)AC = BD,AC ⊥ BD,证明略。
(3)
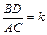 解析:
解析:解:(1)AO = BD,AO⊥BD;

(2)证明:如图4,过点B作BE∥CA交DO于E,∴∠ACO = ∠BEO.
又∵AO = OB,∠AOC = ∠BOE,
∴△AOC ≌ △BOE.∴AC = BE.
又∵∠1 = 45°,∴∠ACO = ∠BEO = 135°.
∴∠DEB = 45°.
∵∠2 = 45°,∴BE = BD,∠EBD = 90°.∴AC = BD.延长AC交DB的延长线于F,如图4.∵BE∥AC,∴∠AFD = 90°.∴AC⊥BD.
(3)如图5,过点B作BE∥CA交DO于E,∴∠BEO = ∠ACO.
又∵∠BOE = ∠AOC ,

∴△BOE ∽ △AOC.
∴
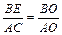 .
.又∵OB = kAO,
由(2)的方法易得 BE = BD.∴
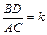 .
. 
练习册系列答案
相关题目
 .
.



 的值.
的值.