题目内容
【题目】如图,∠AOB=∠COD=900,OC平分∠AOB,∠BOD=3∠DOE.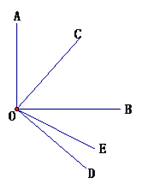
(1)∠DOE的度数;
(2)试求 ∠COE的度数;
【答案】
(1)解: ![]()
![]()
![]()
![]()
![]()
(2)解: ![]()
![]()
![]()
【解析】(1)根据角平分线的定义得出AOC=∠BOC=45° ,根据余角的定义得出∠BOD=45° ,又因∠BOD=3∠DOE ,从而得出∠DOE=45÷3=15 ;
(2)根据角的和差由∠BOE=∠BOD-∠DOE得出∠BOE的度数,再根据∠COE=∠COB+∠BOE得出结果 。
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握角的运算(角之间可以进行加减运算;一个角可以用其他角的和或差来表示)的相关知识才是答题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写大赛”预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m,n的值;
(2)依据数据分析表,有人说:“最高分在九(1)班,九(1)班的成绩比九(2)班好”,但也有人说九(2)班的成绩比较好,请给出两条支持九(2)班成绩好的理由.