题目内容
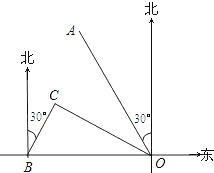
【题目】如图,港口B位于港口O正西方向120海里处,小岛C位于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去.
(1)快艇从港口B到小岛C需要多少时间?
(2)快艇从小岛C出发后最少需要多少时间才能和考察船相遇?
【答案】(1)1小时;(2)1小时.
【解析】
试题分析:(1)要求B到C的时间,已知其速度,则只要求得BC的路程,再利用路程公式即可求得所需的时间.
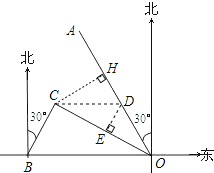
(2)过C作CH⊥OA,垂足为H.设快艇从C岛出发后最少要经过x小时才能和考察船在OA上的D处相遇,则CD=60x,OD=20(x+2).根据直角三角形的性质可解得x的值,从而求得快艇从小岛C出发后和考察船相遇的最短的时间.
试题解析:(1)由题意可知:∠CBO=60°,∠COB=30度.
∴∠BCO=90度.
在Rt△BCO中,
∵OB=120,
∴BC=60,OC=60![]() .
.
∴快艇从港口B到小岛C的时间为:60÷60=1(小时).
(2)设快艇从C岛出发后最少要经过x小时才能和考察船在OA上的D处相遇,则CD=60x.
过点D作DE⊥CO于点E,
∵考察船与快艇是同时出发,
∵快艇从港口B到小岛C的时间是1小时,在小岛C用1小时装补给物资,
∴考察船从O到D行驶了(x+2)小时,
∴OD=20(x+2).
过C作CH⊥OA,垂足为H,
在△OHC中,
∵∠COH=30°,OB=120,
∴CO=60![]() ,
,
∴CH=30![]() ,OH=90.
,OH=90.
∴DH=OH-OD=90-20(x+2)=50-20x.
在Rt△CHD中,CH2+DH2=CD2,
∴(30![]() )2+(50-20x)2=(60x)2.
)2+(50-20x)2=(60x)2.
整理得:8x2+5x-13=0.
解得:x1=1,x2=-![]() .
.
∵x>0,
∴x=1.
答:快艇从小岛C出发后最少需要1小时才能和考察船相遇.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案