题目内容
【题目】如图，将放置于直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A1OB1．已知∠AOB=30°，∠B=90°，AB=1，则B1点的坐标为（ ）
A. (
，
) B. （
，） C. （，） D （，）
【答案】D
【解析】由于在Rt△ABO中，∠AOB=30°，∠B=90°，AB=1，由此分别求出B的坐标，然后根据旋转的性质即可求出B′的坐标．
解：如图，过B作BC⊥OA于C，
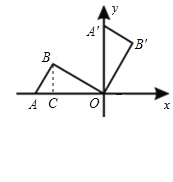
在Rt△ABO中，∠AOB=30°，∠ABO=90°，AB=1，∴AO=2 BO=，
在Rt△BCO中，BC=
,OC=
而三角板AOB绕O点顺时针旋转90°得△A′OB′∴B′点的坐标为（，)
故选D．
“点睛”此题主要考查了旋转的性质及坐标与图形变换，同时也利用了直角三角形性质，首先利用直角三角形的性质得到有关线段的长度，然后利用旋转的性质即可解决问题．
练习册系列答案
阅读快车系列答案
相关题目
