题目内容
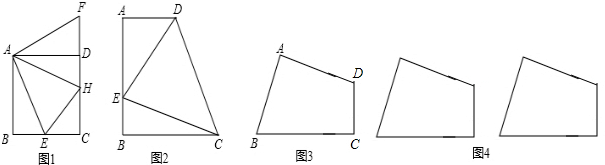
如图1,在正方形ABCD内有一点P,PA=
,PB=
,PC=1,求∠BPC的度数.
【分析问题】根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
【解决问题】请你通过计算求出图2中∠BPC的度数;
【比类问题】如图3,若在正六边形ABCDEF内有一点P,且PA=2
,PB=4,PC=2.
(1)∠BPC的度数为
(2)直接写出正六边形ABCDEF的边长为

| 5 |
| 2 |
【分析问题】根据已知条件比较分散的特点,我们可以通过旋转变换将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
【解决问题】请你通过计算求出图2中∠BPC的度数;
【比类问题】如图3,若在正六边形ABCDEF内有一点P,且PA=2
| 13 |
(1)∠BPC的度数为
120°
120°
; (2)直接写出正六边形ABCDEF的边长为
2
| 7 |
2
.| 7 |

分析:【解决问题】如图4,将△PBC逆时针旋转90°得△P′BA,连接PP′,就可以求得∠P′BP=90°,P′B=PB,求出∠BP′P的度数,由勾股定理就可以求出PP′的值,在△P′AP中由勾股定理的逆定理可以得出△P′AP是直角三角形,求出∠PP′A的度数,从而可以求出结论;
(1)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,然后连结PP′.如图所示,根据旋转的性质可得:△PBC≌△P′BA,从而得出△BPP′为等腰三角形,PB=P′B=4,PC=P′A=2,∠BPC=∠BP′A,由∠ABC=120°,就有∠PBP′=120°,∠BP′P=30°,可以求得PP′=4
,由勾股定理的逆定理就可以求出∠AP′P=90°从而得出结论;
(2)延长A P′作BG⊥AP′于点G,在Rt△P′BG中,P′B=4,∠BP′G=60°,就可以得出P′G=2,BG=2
,则AG=P′G+P′A=2+2=4,在Rt△ABG中,根据勾股定理得AB=2
.
(1)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,然后连结PP′.如图所示,根据旋转的性质可得:△PBC≌△P′BA,从而得出△BPP′为等腰三角形,PB=P′B=4,PC=P′A=2,∠BPC=∠BP′A,由∠ABC=120°,就有∠PBP′=120°,∠BP′P=30°,可以求得PP′=4
| 3 |
(2)延长A P′作BG⊥AP′于点G,在Rt△P′BG中,P′B=4,∠BP′G=60°,就可以得出P′G=2,BG=2
| 3 |
| 7 |
解答:解:【解决问题】如图4,将△PBC逆时针旋转90°得△P′BA,连接PP′,
∴△AP′B≌△CPB,
∴P′B=PB=
,P′A=PC=1,∠1=∠2.∠AP′B=∠BPC.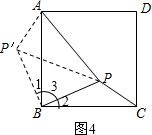
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠1+∠3=90°,
即∠P′BP=90°.
∴∠BP′P=45°.
在Rt△P′BP中,由勾股定理,得
PP′2=4.
∵P′A=1,AP=
∴P′A2=1,AP2=5,
∴P′A2+PP′2=AP2,
∴△P′AP是直角三角形,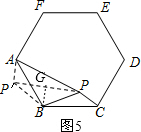
∴∠AP′P=90°.
∴∠AP′B=45°+90°=135°,
∴∠BPC=135°;
(1)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,连结PP′.如图5,
∴△PBC≌△P′BA,
∴P′B=PB=4,PC=P′A=2,∠BPC=∠BP′A,
∴△BPP′为等腰三角形,
∵∠ABC=120°,
∴∠PBP′=120°,
∴∠BP′P=30°,
作BG⊥PP′于G,
∴∠P′GB=90°,PP′=2P′G.
∵P′B=PB=4,∠BP′P=30°,
∴BG=2,
∴P′G=2
∴PP′=4
,
在△APP′中,∵PA=2
,PP′=4
,P′A=2,
∴PA2=52,PP′2=48,P′A2=4,
∴P′A2+P′P2=PA2,
∴△PP′A是直角三角形,
∴∠AP′P=90°.
∴∠BPC=∠BP′A=30°+90°=120°.
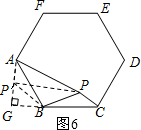
(2)延长A P′作BG⊥AP′于点G,如图6,
在Rt△P′BG中,P′B=4,∠BP′G=60°,
∴P′G=2,BG=2
,
∴AG=P′G+P′A=2+2=4,
在Rt△ABG中,根据勾股定理得AB=2
.
故答案为:120°;2
.
∴△AP′B≌△CPB,
∴P′B=PB=
| 2 |

∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠1+∠3=90°,
即∠P′BP=90°.
∴∠BP′P=45°.
在Rt△P′BP中,由勾股定理,得
PP′2=4.
∵P′A=1,AP=
| 5 |
∴P′A2=1,AP2=5,
∴P′A2+PP′2=AP2,
∴△P′AP是直角三角形,

∴∠AP′P=90°.
∴∠AP′B=45°+90°=135°,
∴∠BPC=135°;
(1)仿照【分析】中的思路,将△BPC绕点B逆时针旋转120°,得到了△BP′A,连结PP′.如图5,
∴△PBC≌△P′BA,
∴P′B=PB=4,PC=P′A=2,∠BPC=∠BP′A,
∴△BPP′为等腰三角形,
∵∠ABC=120°,
∴∠PBP′=120°,
∴∠BP′P=30°,
作BG⊥PP′于G,
∴∠P′GB=90°,PP′=2P′G.
∵P′B=PB=4,∠BP′P=30°,
∴BG=2,
∴P′G=2
| 3 |

∴PP′=4
| 3 |
在△APP′中,∵PA=2
| 13 |
| 3 |
∴PA2=52,PP′2=48,P′A2=4,
∴P′A2+P′P2=PA2,
∴△PP′A是直角三角形,
∴∠AP′P=90°.
∴∠BPC=∠BP′A=30°+90°=120°.
(2)延长A P′作BG⊥AP′于点G,如图6,
在Rt△P′BG中,P′B=4,∠BP′G=60°,
∴P′G=2,BG=2
| 3 |
∴AG=P′G+P′A=2+2=4,
在Rt△ABG中,根据勾股定理得AB=2
| 7 |
故答案为:120°;2
| 7 |
点评:本题是一道四边形的综合试题,考查了旋转在正多边形中的运用,全等三角形的判定及性质的运用,勾股定理的运用,勾股定理的逆定理的运用,等腰三角形的性质的运用,解答本题时运用等腰三角形的性质解答是关键

练习册系列答案
相关题目

 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明. 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.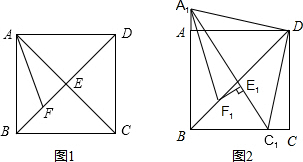 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.