题目内容
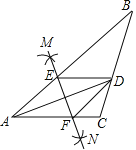
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于![]() AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,求线段BE的长.

【答案】8
【解析】
根据作法得到MN是线段AD的垂直平分线,则AE=DE,AF=DF,所以∠EAD=∠EDA,加上∠BAD=∠CAD,得到∠EDA=∠CAD,则可判断DE∥AC,同理DF∥AE,于是可判断四边形AEDF是平行四边形,加上EA=ED,则可判断四边形AEDF为菱形,所以AE=DE=DF=AF=4,然后利用平行线分线段成比例可计算BE的长.
解:根据作法可知:MN是线段AD的垂直平分线,
∴AE=DE,AF=DF
,
∴∠EAD=∠EDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠EDA=∠CAD,
∴DE∥AC,
同理DF∥AE,
∴四边形AEDF是平行四边形,
而EA=ED,
∴四边形AEDF为菱形,
∴AE=DE=DF=AF=4,
∵DE∥AC,
∴BE:AE=BD:CD,即BE:4=6:3,
∴BE=8.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?