题目内容
 如图,已知点A的坐标为(
如图,已知点A的坐标为(| 3 |
| k |
| x |
| 5 |
| 4 |
分析:根据A点的坐标为(
,3)、AB=3BD,可以求得点D的坐标,从而得出反比例函数y=
解析式,再根据A点坐标得出AO直线解析式,进而得出两图象的交点坐标,进而得出AC的长度,再利用直线与圆的位置关系得出答案.
| 3 |
| k |
| x |
解答: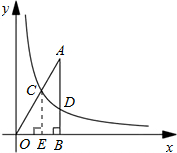 解:∵已知点A的坐标为(
解:∵已知点A的坐标为(
,3),AB=3BD,
∴AB=3,BD=1,
∴D点的坐标为(
,1),
∴反比例函数y=
解析式为:
y=
,
∴AO直线解析式为:y=kx,
3=
k,
∴k=
,
∴y=
x,
∴直线y=
x与反比例函数y=
的交点坐标为:
x=±1,
∴C点的横坐标为1,纵坐标为
,
过C点做CE垂直于OB于点E,
则CO=2,
∴AC=2
-2,
∴CA的
倍=
(
-1),
CE=
,
∵
(
-1)-
=
-
>0,
∴该圆与x轴的位置关系是相交.
故选:C.
 解:∵已知点A的坐标为(
解:∵已知点A的坐标为(| 3 |
∴AB=3,BD=1,
∴D点的坐标为(
| 3 |
∴反比例函数y=
| k |
| x |
y=
| ||
| x |
∴AO直线解析式为:y=kx,
3=
| 3 |
∴k=
| 3 |
∴y=
| 3 |
∴直线y=
| 3 |
| ||
| x |
x=±1,
∴C点的横坐标为1,纵坐标为
| 3 |
过C点做CE垂直于OB于点E,
则CO=2,
∴AC=2
| 3 |
∴CA的
| 5 |
| 4 |
| 5 |
| 2 |
| 3 |
CE=
| 3 |
∵
| 5 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 5 |
| 2 |
∴该圆与x轴的位置关系是相交.
故选:C.
点评:此题主要考查了直线与圆的位置关系以及反比例函数的性质以及直线与反比例函数交点坐标的求法,综合性较强得出AC的长是解决问题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
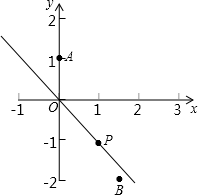 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
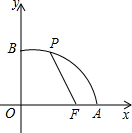 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-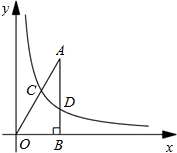 如图,已知点A的坐标为(
如图,已知点A的坐标为(
