题目内容
 如图,已知点A的坐标为(
如图,已知点A的坐标为(| 3 |
| ||
| x |
3+
| ||
| 4 |
3+
| ||
| 4 |
分析:先根据勾股定理求出OA的长,再利用待定系数法求出直线OA的解析式,故可得出C点坐标,过点C作CE⊥x轴于点E,则△OAB∽△OCE,再由相似三角形的对应边成比例即可求出OC的长,进而得出CA的长,故可得出结论.
解答: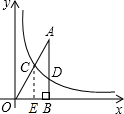 解:∵点A的坐标为(
解:∵点A的坐标为(
,3),AB⊥x轴,垂足为B,
∴OA=
=
=2
,
设直线OA的解析式为y=kx(k≠0),
∵点A的坐标为(
,3),
∴
k=3,解得k=
,
∴直线OA的解析式为y=
x(k≠0),
∴
,解得
,
∴C(1,
),
过点C作CE⊥x轴于点E,
∵AB⊥x轴,
∴△OAB∽△OCE,
∴
=
,即
=
,解得OC=2,
∴CA=OA-OC=2
-2=2(1-
),
∵以点C为圆心,CA的k倍的长为半径作圆,该圆与x轴相切,
∴kCA=CE,即2(1-
)=
,解得k=
.
故答案为:
.
 解:∵点A的坐标为(
解:∵点A的坐标为(| 3 |
∴OA=
| AB2+OB2 |
32+(
|
| 3 |
设直线OA的解析式为y=kx(k≠0),
∵点A的坐标为(
| 3 |
∴
| 3 |
| 3 |
∴直线OA的解析式为y=
| 3 |
∴
|
|
∴C(1,
| 3 |
过点C作CE⊥x轴于点E,
∵AB⊥x轴,
∴△OAB∽△OCE,
∴
| OC |
| OA |
| CE |
| AB |
| OC | ||
2
|
| ||
| 3 |
∴CA=OA-OC=2
| 3 |
| 3 |
∵以点C为圆心,CA的k倍的长为半径作圆,该圆与x轴相切,
∴kCA=CE,即2(1-
| 3 |
| 3 |
3+
| ||
| 4 |
故答案为:
3+
| ||
| 4 |
点评:本题考查的是反比例函数综合题,熟知反比例函数的性质是解答此题的关键.

练习册系列答案
相关题目
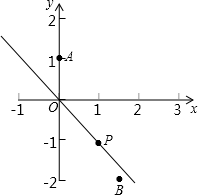 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
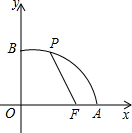 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-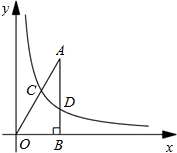 如图,已知点A的坐标为(
如图,已知点A的坐标为(
