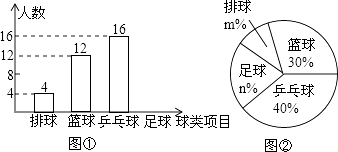
题目内容
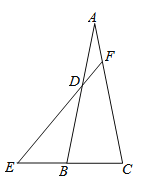
【题目】如图,△ABC是等腰三角形,AB=AC=3,BC=1.点D在AB边上,点E在CB的延长线上,已知AD=1,BE=1,连接ED并延长交AC于点F,则线段AF的长为_________.
【答案】![]()
【解析】
取CF的中点G,连接BG,证出BG是△CEF的中位线,由三角形中位线定理得出BG∥EF,证出△ADF∽△ABG,得出比例式![]() ,因此AF=
,因此AF=![]() AG,∴FG=CG=2AF,得出AC=AF+FG+CG=5AF=3,即可得出AF的长.
AG,∴FG=CG=2AF,得出AC=AF+FG+CG=5AF=3,即可得出AF的长.
取CF的中点G,连接BG,如图所示:
∵BC=1,BE=1,
∴点B为EC的中点,
∴BG是△CEF的中位线,
∴BG∥EF,
∴![]() ,
,
∴AF=![]() AG,
AG,
∴FG=CG=2AF,
∴AC=AF+FG+CG=5AF=3,
∴AF=![]() ;
;
故答案为:![]()

练习册系列答案
相关题目