题目内容
如图,平面直角坐标系中,四边形OABC为矩形,点( )
A.B的坐标分别为(6,0),(6,8)。动点M、N分别从O、B同时出发,以每秒1个单位的速度运动。其中,点M沿OA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于P,连结MP。已知动点运动了x秒。
(1)P点的坐标为(_____________,_______________);(用含x的代数式表示)
(2)试求 MPA面积的最大值,并求此时x的值。
(3)请你探索:当x为何值时,MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果。
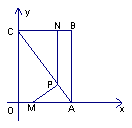
(1)(6―x , ![]() x ); (2)设MPA的面积为S,在MPA中,MA=6―x,MA边上的高为
x ); (2)设MPA的面积为S,在MPA中,MA=6―x,MA边上的高为![]() x,其中,0≤x≤6.∴S=
x,其中,0≤x≤6.∴S=![]() (6―x)×
(6―x)×![]() x=
x=![]() (―x2+6x) = ―
(―x2+6x) = ― ![]() (x―3)2+6
(x―3)2+6
∴S的最大值为6, 此时x =3. (3)延长NP交x轴于Q,则有PQ⊥OA
①若MP=PA ∵PQ⊥MA ∴MQ=QA=x. ∴3x=6, ∴x=2;
②若MP=MA,则MQ=6―2x,PQ=![]() x,PM=MA=6―x
x,PM=MA=6―x
在RtPMQ 中,∵PM2=MQ2+PQ2 ∴(6―x) 2=(6―2x) 2+ (![]() x) 2∴x=
x) 2∴x=![]()
③若PA=AM,∵PA=![]() x,AM=6―x ∴
x,AM=6―x ∴![]() x=6―x ∴x=
x=6―x ∴x=![]()
综上所述,x=2,或x=![]() ,或x=
,或x=![]() 。
。

练习册系列答案
相关题目
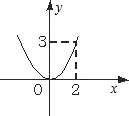 如图平面直角坐标系中,函数图象的表达式应是( )
如图平面直角坐标系中,函数图象的表达式应是( )A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
 11、象棋中的马走日字对角(如图1由点A到点B或由点A到点C),现建立如图2平面直角坐标系,则下一步可能到达的点的坐标是
11、象棋中的马走日字对角(如图1由点A到点B或由点A到点C),现建立如图2平面直角坐标系,则下一步可能到达的点的坐标是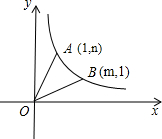 OA、OB.
OA、OB. 如图平面直角坐标系中,已知点A的坐标为(-3,-1),点B的坐标为(2,-4).
如图平面直角坐标系中,已知点A的坐标为(-3,-1),点B的坐标为(2,-4). 在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),
在如图平面直角坐标系中,△ABC三个顶点A、B、C的坐标分别为A(2,-1),B(1,-3),C(4,-4),