题目内容
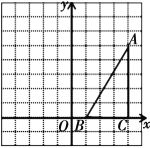
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
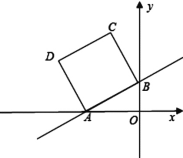
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)在x轴上找一点M,使△MDB的周长最小,请求出M点的坐标.
【答案】(1)![]() ;(2)D(-6,4);(3)M(-2,0)
;(2)D(-6,4);(3)M(-2,0)
【解析】
(1)由题意将y=0和x=0分别代入即可求出点A、B的坐标,进而求出边AB的长;
(2)根据题意作DH⊥![]() 轴于H,并利用全等三角形的判定与性质求得△DAH≌△ABO,进而得出DH和OH的值即可;
轴于H,并利用全等三角形的判定与性质求得△DAH≌△ABO,进而得出DH和OH的值即可;
(3)根据题意作D点关于![]() 轴的对称点为E,并连接BE交x轴于点M,△MDB的周长为
轴的对称点为E,并连接BE交x轴于点M,△MDB的周长为![]() ,有
,有![]() 为定值,只需满足
为定值,只需满足![]() 的值最小即可,将
的值最小即可,将![]() 进行转化,根据两点间线段最短即可知道此时的M即为所求,解出直线BE的解析式即可得到M点的坐标.
进行转化,根据两点间线段最短即可知道此时的M即为所求,解出直线BE的解析式即可得到M点的坐标.
解:(1)由题意直线y=![]() x+2与x轴、y轴分别交于A、B两点,将y=0和x=0分别代入即可求出点A、B的坐标为:A(-4,0),B(0,2),
x+2与x轴、y轴分别交于A、B两点,将y=0和x=0分别代入即可求出点A、B的坐标为:A(-4,0),B(0,2),
所以AB=![]() .
.
(2)作DH⊥![]() 轴于H,
轴于H,
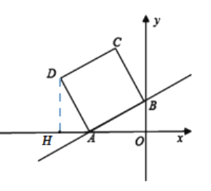
由于∠DHA=∠BAD=90°,
∠DAH+∠BAO=90°,
∠BAO+∠ABO=90°,
∴∠DAH=∠ABO,
又DA=AB,
∴△DAH≌△ABO(AAS),
则DH=OA=4,AH=OB=2,OH=4+2=6,
∵点D的坐标在第二象限,
∴D(-6,4).
(3)作D点关于![]() 轴的对称点为E,并连接BE交x轴于点M,
轴的对称点为E,并连接BE交x轴于点M,
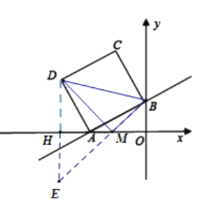
根据轴对称的性质可知![]() ,E(-6,-4),
,E(-6,-4),
△MDB的周长为:![]() ,有
,有![]() 为定值,只需满足
为定值,只需满足![]() 的值最小即可,
的值最小即可,
将![]() 进行转化,根据两点间线段最短即可知道此时的M即为所求,
进行转化,根据两点间线段最短即可知道此时的M即为所求,
利用待定系数法求得直线BE的解析式为![]() ,
,
直线![]() 与
与![]() 轴的交点坐标为(-2,0),
轴的交点坐标为(-2,0),
故M(-2,0).

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目