题目内容
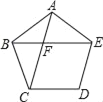
【题目】如图，在正五边形ABCDE中，对角线AC，BE相交于点F，F是线段BE、AC的黄金分割线吗？为什么？
【答案】见解析
【解析】
根据正五边形的性质得到∠ABC=∠BAE=108°，AB=BC=AE，则利用三角形内角和和等腰三角形的性质计算出∠BAC=∠BCA=36°，∠ABE=∠AEB=36°，易得∠CBF=72°，∠CFB=72°，所以CB=CF，再证明△ABF∽△ACB，则AB：AC=AF：AB，所以CF：AC=AF：CF，根据黄金分割的定义得到点F是线段AC的黄金分割点，用同样的方法可得F是线段BE的黄金分割点．
解：F是线段BE、AC的黄金分割点．理由如下：
∵五边形ABCDE是正五边形，
∴∠ABC=∠BAE=108°，AB=BC=AE，
∴∠BAC=∠BCA=36°，∠ABE=∠AEB=36°，
∴∠CBF=72°，∠CFB=72°，
∴CB=CF，
∵∠ABF=∠ACB=36°，
∴△ABF∽△ACB，
∴AB：AC=AF：AB，
∴CF：AC=AF：CF，
∴点F是线段AC的黄金分割点，
同理可得F是线段BE的黄金分割点．
练习册系列答案
相关题目
【题目】当前，“校园ipad现象已经受到社会的广泛关注，某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查．小文将调查数据作出如下不完整的整理：
频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |
（1）请求出共调查了多少人；并把小文整理的图表补充完整；
（2）小丽要将调查数据绘制成扇形统计图，则扇形图中“赞成”的圆心角是多少度？
（3）若该校有3000名学生，请您估计该校持“反对”态度的学生人数．
