题目内容
【题目】在△ABC中，AB=6，AC=8，BC=10，D是△ABC内部或BC边上的一个动点（与B、C不重合），以D为顶点作△DEF，使△DEF∽△ABC（相似比k＞1），EF∥BC．
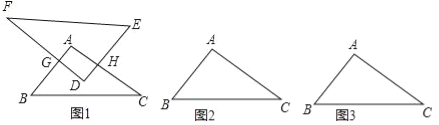
（1）求∠D的度数；
（2）若两三角形重叠部分的形状始终是四边形AGDH．
①如图1，连接GH、AD，当GH⊥AD时，请判断四边形AGDH的形状，并证明；
②当四边形AGDH的面积最大时，过A作AP⊥EF于P，且AP=AD，求k的值．
【答案】（1）90°；（2）①四边形AGDH为正方形，理由详见解析；②k=
．
【解析】
试题分析：（1）根据已知条件，由勾股定理的逆定理判定△ABC是直角三角形，即可证得结论；（2）①先判断AB∥DE，DF∥AC，得到平行四边形，再判断出是正方形；②先判断面积最大时点D的位置，由△BGD∽△BAC，找出AH=8﹣
GA，得到S矩形AGDH=﹣
AG2+8AG，确定极值，AG=3时，面积最大，最后求k得值．
试题解析：（1）∵AB2+AC2=100=BC2，
∴∠BAC=90°，
∵△DEF∽△ABC，
∴∠D=∠BAC=90°，
（2）①四边形AGDH为正方形，
理由：如图1，
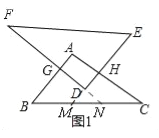
延长ED交BC于M，延长FD交BC于N，
∵△DEF∽△ABC，
∴∠B=∠C，
∵EF∥BC，
∴∠E=∠EMC，
∴∠B=∠EMC，
∴AB∥DE，
同理：DF∥AC，
∴四边形AGDH为平行四边形，
∵∠D=90°，
∴四边形AGDH为矩形，
∵GH⊥AD，
∴四边形AGDH为正方形；
②当点D在△ABC内部时，四边形AGDH的面积不可能最大，
理由：如图2，
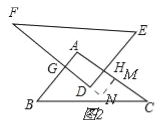
点D在内部时（N在△ABC内部或BC边上），延长GD至N，过N作NM⊥AC于M，
∴矩形GNMA面积大于矩形AGDH，
∴点D在△ABC内部时，四边形AGDH的面积不可能最大，
只有点D在BC边上时，面积才有可能最大，
如图3，
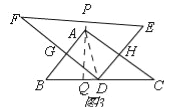
点D在BC上，
∵DG∥AC，
∴△BGD∽△BAC，
∴
，
∴
，
∴
，
∴AH=8﹣GA，
S矩形AGDH=AG×AH=AG×（8﹣AG）=﹣AG2+8AG，
当AG=﹣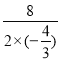
=3时，S矩形AGDH最大，此时，DG=AH=4，
即：当AG=3，AH=4时，S矩形AGDH最大，
在Rt△BGD中，BD=5，
∴DC=BC﹣BD=5，
即：点D为BC的中点，
∵AD=
BC=5，
∴PA=AD=5，
延长PA，∵EF∥BC，QP⊥EF，
∴QP⊥BC，
∴PQ是EF，BC之间的距离，
∴D是EF的距离为PQ的长，
在△ABC中，
AB×AC=BC×AQ
∴AQ=4.8
∵△DEF∽△ABC，
∴k=
．
