题目内容
（2013•绥化）如图，点A，B，C，D为⊙O上的四个点，AC平分∠BAD，AC交BD于点E，CE=4，CD=6，则AE的长为（ ）分析：根据圆周角定理∠CAD=∠CDB，继而证明△ACD∽△DCE，设AE=x，则AC=x+4，利用对应边成比例，可求出x的值．
解答：解：设AE=x，则AC=x+4，
∵AC平分∠BAD，
∴∠BAC=∠CAD，
∵∠CDB=∠BAC（圆周角定理），
∴∠CAD=∠CDB，
∵∠ACD=∠ACD，
∴△ACD∽△DCE，
∴
=
，即
=
，
解得：x=5．
故选B．
∵AC平分∠BAD，
∴∠BAC=∠CAD，
∵∠CDB=∠BAC（圆周角定理），
∴∠CAD=∠CDB，
∵∠ACD=∠ACD，
∴△ACD∽△DCE，
∴
| CD |
| CE |
| AC |
| DC |
| 6 |
| 4 |
| x+4 |
| 6 |
解得：x=5．
故选B．
点评：本题考查了圆周角定理、相似三角形的判定与性质，解答本题的关键是得出∠CAD=∠CDB，证明△ACD∽△DCE．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
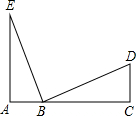（2013•绥化）如图，A，B，C三点在同一条直线上，∠A=∠C=90°，AB=CD，请添加一个适当的条件
（2013•绥化）如图所示，以O为端点画六条射线后OA，OB，OC，OD，OE，O后F，再从射线OA上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6，7，8…后，那么所描的第2013个点在射线
（2013•绥化）如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E，F分别是边AD，AB的中点，EF交AC于点H，则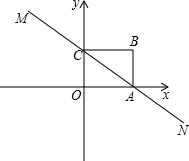
（2013•绥化）如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2-14x+48=0的两个实数根．