题目内容
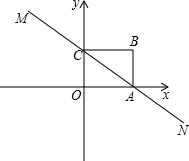 (2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.
(2013•绥化)如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根.(1)求C点坐标;
(2)求直线MN的解析式;
(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.
分析:(1)通过解方程x2-14x+48=0可以求得OC=6,OA=8.则C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
(2)设直线MN的解析式是y=kx+b(k≠0).把点A、C的坐标分别代入解析式,列出关于系数k、b的方程组,通过解方程组即可求得它们的值;
(3)需要分类讨论:PB为腰,PB为底两种情况下的点P的坐标.根据等腰三角形的性质、两点间的距离公式以及一次函数图象上点的坐标特征进行解答.
解答: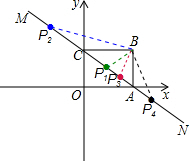 解:(1)解方程x2-14x+48=0得
解:(1)解方程x2-14x+48=0得
x1=6,x2=8.
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根,
∴OC=6,OA=8.
∴C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).
由(1)知,OA=8,则A(8,0).
∵点A、C都在直线MN上,
∴
,
解得,
,
∴直线MN的解析式为y=-
x+6;
(3)∵A(8,0),C(0,6),
∴根据题意知B(8,6).
∵点P在直线MNy=-
x+6上,
∴设P(a,-
a+6)
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-
a+6-6)2=64,
解得,a=±
,则P2(-
,
),P3(
,
);
③当PB=BC时,(a-8)2+(-
a+6-6)2=64,
解得,a=
,则-
a+6=-
,∴P4(
,-
).
综上所述,符合条件的点P有:P1(4,3),P2(-
,
)P3(
,
),P4(
,-
).
 解:(1)解方程x2-14x+48=0得
解:(1)解方程x2-14x+48=0得x1=6,x2=8.
∵OA,OC(OA>OC)的长分别是一元二次方程x2-14x+48=0的两个实数根,
∴OC=6,OA=8.
∴C(0,6);
(2)设直线MN的解析式是y=kx+b(k≠0).
由(1)知,OA=8,则A(8,0).
∵点A、C都在直线MN上,
∴
|
解得,
|
∴直线MN的解析式为y=-
| 3 |
| 4 |
(3)∵A(8,0),C(0,6),
∴根据题意知B(8,6).
∵点P在直线MNy=-
| 3 |
| 4 |
∴设P(a,-
| 3 |
| 4 |
当以点P,B,C三点为顶点的三角形是等腰三角形时,需要分类讨论:
①当PC=PB时,点P是线段BC的中垂线与直线MN的交点,则P1(4,3);
②当PC=BC时,a2+(-
| 3 |
| 4 |
解得,a=±
| 32 |
| 5 |
| 32 |
| 5 |
| 54 |
| 5 |
| 32 |
| 5 |
| 6 |
| 5 |
③当PB=BC时,(a-8)2+(-
| 3 |
| 4 |
解得,a=
| 256 |
| 25 |
| 3 |
| 4 |
| 42 |
| 25 |
| 256 |
| 25 |
| 42 |
| 25 |
综上所述,符合条件的点P有:P1(4,3),P2(-
| 32 |
| 5 |
| 54 |
| 5 |
| 32 |
| 5 |
| 6 |
| 5 |
| 256 |
| 25 |
| 42 |
| 25 |
点评:本题考查了一次函数综合题.其中涉及到的知识点有:待定系数法求一次函数解析式,一次函数图象上点的坐标特征,等腰三角形的性质.解答(3)题时,要分类讨论,防止漏解.另外,解答(3)题时,还利用了“数形结合”的数学思想.

练习册系列答案
相关题目
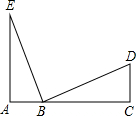 (2013•绥化)如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件
(2013•绥化)如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件 (2013•绥化)如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线
(2013•绥化)如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线 (2013•绥化)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则
(2013•绥化)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则 (2013•绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为( )
(2013•绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为( )