Question

【题目】如图所示，直四棱柱ABCD﹣A1B1C1D1内接于半径为 的半球O，四边形ABCD为正方形，则该四棱柱的体积最大时，AB的长是（ ）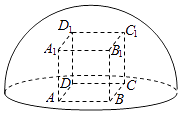
A.1
B.
C.
D.2

Answer 1

【答案】D
【解析】解：设AB=a，BB1=h， 则OB= a，连接OB1 ， OB，则OB2+BB12=OB12=3，
∴ =3，
∴a2=6﹣2h2 ，
故正四棱柱的体积是V=a2h=6h﹣2h3 ，
∴V′=6﹣6h2 ，
当0＜h＜1时，V′＞0，1＜h＜ 时，V′＜0，
∴h=1时，该四棱柱的体积最大，此时AB=2．
故选：D．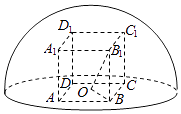

设AB=a，BB1=h，求出a2=6﹣2h2 ， 故正四棱柱的体积是V=a2h=6h﹣2h3 ， 利用导数，得到该正四棱柱体积的最大值，即可得出结论．