Question

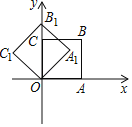
【题目】如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F.

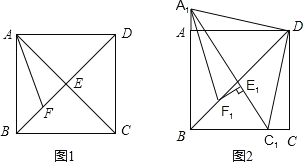
(1)求证：EF+AC=AB；

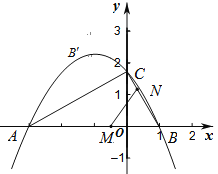
(2)点C1从点C出发，沿着线段CB向点B运动(不与点B重合)，同时点A1从点A出发，沿着BA的延长线运动，点C1与A1的运动速度相同，当动点C1停止运动时，另一动点A1也随之停止运动。如图2，A1F1平分∠BA1C1，交BD于点F1，过点F1作F1E1⊥A1C1，垂足为E1，请猜想E1F1，A1C1与AB三者之间的数量关系，并证明你的猜想；

(3)在(2)的条件下，当A1E1=3，C1E1=2时，求BD的长。

Answer 1

【答案】（1）见解析；（2）见解析；（3）BD=

【解析】

（1）过F作FM⊥AB于点M，首先证明△AMF≌△AEF，求出MF=MB，即可知道EF+AE=AB．

（2）连接F1C1，过点F1作F1P⊥A1B于点P，F1Q⊥BC于点Q，证明Rt△A1E1F1≌Rt△A1PF1，Rt△QF1C1≌Rt△E1F1C1后推出A1B+BC1=A1P+PB+QB+C1Q=A1P+C1Q+2E1F1化简为E1F1+A1C1=AB．

（3）设PB=x，QB=x，PB=1，E1F1=1，又推出E1F1+A1C1=AB，得出BD= .

(1)证明：如图1，过点F作FM⊥AB于点M，在正方形ABCD中，AC⊥BD于点E.

∴AE=AC,∠ABD=∠CBD=45°，

∵AF平分∠BAC，

∴EF=MF，

又∵AF=AF，

∴Rt△AMF≌Rt△AEF，

∴AE=AM，

∵∠MFB=∠ABF=45°，

∴MF=MB，MB=EF，

∴EF+AC=MB+AE=MB+AM=AB.

(2)E1F1, A1C1与AB三者之间的数量关系：E1F1+A1C1=AB

证明：如图2,连接F1C1,过点F1作F1P⊥A1B于点P,F1Q⊥BC于点Q，

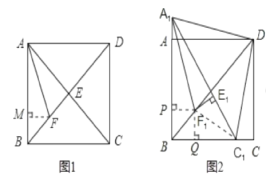
∵A1F1平分∠BA1C1,∴E1F1=PF1;同理QF1=PF1,∴E1F1=PF1=QF1，

又∵A1F1=A1F1,∴Rt△A1E1F1≌Rt△A1PF1，

∴A1E1=A1P，

同理Rt△QF1C1≌Rt△E1F1C1，

∴C1Q=C1E1，

由题意：A1A=C1C，

∴A1B+BC1=AB+A1A+BCC1C=AB+BC=2AB，

∵PB=PF1=QF1=QB，

∴A1B+BC1=A1P+PB+QB+C1Q=A1P+C1Q+2E1F1，

即2AB=A1E1+C1E1+2E1F1=A1C1+2E1F1，

∴E1F1+A1C1=AB.

(3)设PB=x，则QB=x，

∵A1E1=3,QC1=C1E1=2，

Rt△A1BC1中,A1B2+BC12=A1C12，

即(3+x)2+(2+x)2=52，

∴x1=1,x2=6(舍去)，

∴PB=1，

∴E1F1=1，

又∵A1C1=5，

由(2)的结论：E1F1+A1C1=AB，

∴AB= ，

∴BD=.