Question

【题目】要在一块长52 m，宽48 m的矩形绿地上，修建同样宽的两条互相垂直的甬路，下面分别是小亮和小颖的设计方案．

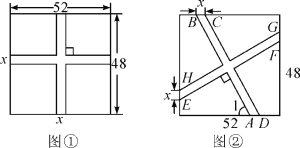
小亮设计的方案如图①所示，甬路宽度均为x m，剩余的四块绿地面积共2300 m2.

小颖设计的方案如图②所示，BC＝HE＝x，AB∥CD，HG∥EF，AB⊥EF，∠1＝60°.

(1)求小亮设计方案中甬路的宽度x；

(2)求小颖设计方案中四块绿地的总面积．(友情提示：小颖设计方案中的x与小亮设计方案中的x取值相同)

Answer 1

【答案】（1）小亮设计方案中甬路的宽度为2 m；（2）小颖设计方案中四块绿地的总面积为2299m2.

【解析】

(1)根据小亮的设计方案列方程得(52－x)(48－x)＝2 300，解方程可得；

（2）先证四边形ADCB为平行四边形，由(1)得x＝2， BC＝HE＝2＝AD，过点A作AI⊥CD于点I，则ID＝AD＝1，AI＝，则小颖设计方案中四块绿地的总面积＝52×48－52×2－48×2＋()2.

解：(1)根据小亮的设计方案列方程得(52－x)(48－x)＝2 300，解得x1＝2，x2＝98(舍去)，

∴小亮设计方案中甬路的宽度为2 m.

(2)易证四边形ADCB为平行四边形，由(1)得x＝2，

∴BC＝HE＝2＝AD，过点A作AI⊥CD于点I，则ID＝AD＝1，

∴AI＝，

∴小颖设计方案中四块绿地的总面积＝52×48－52×2－48×2＋()2＝2 299(m2).