题目内容
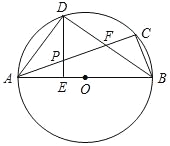
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)求证:∠DAC=∠DBA;
(2)求证:PD=PF;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
【答案】(1)证明见解析;(2)证明见解析;(3)半径为2.5;DE=2.4;
【解析】
(1)、利用角平分线的性质得出∠CBD=∠DBA,进而得出∠DAC=∠DBA,再利用互余的性质得出∠DAC=∠ADE,进而得出∠DAC=∠DBA;(2)、利用圆周角定理得出∠ADB=90°,进而求出∠PDF=∠PFD,则PD=PF;(3)、利用勾股定理得出AB的长,再利用三角形面积求出DE即可.
(1)、证明:∵BD平分∠CBA,∴∠CBD=∠DBA,∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,∴∠DAC=∠DBA,∵AB是⊙O的直径,DE⊥AB,∴∠ADB=∠AED=90°,
∴∠ADE+∠DAE=90°,∠DBA+∠DAE=90°,∴∠ADE=∠DBA,∴∠DAC=∠ADE,∴∠DAC=∠DBA;
(2)、证明:∵AB为直径,∴∠ADB=90°,∵DE⊥AB于E,∴∠DEB=90°,
∴∠ADE+∠EDB=∠DFA+∠DAC =90°,又∵∠ADE =∠DAP,∴∠PDF=∠PFD,∴PD=PF,
(3)、连接CD,∵∠CBD=∠DBA,∴CD=AD,∵CD﹦3,∴AD=3,∵∠ADB=90°,∴AB=5,
故⊙O的半径为2.5,∵DE×AB=AD×BD,∴5DE=3×4,∴DE=2.4. 即DE的长为2.4.

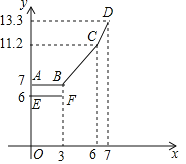
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.