题目内容
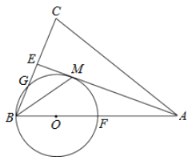
【题目】如图,正方形ABCD的边长为4,点E在边AB上,BE=1,∠DAM=45°,点F在射线AM上,且AF=![]() ,过点F作AD的平行线交BA的延长线于点H,CF与AD相交于点G,连接EC、EG、EF.下列结论:①△ECF的面积为
,过点F作AD的平行线交BA的延长线于点H,CF与AD相交于点G,连接EC、EG、EF.下列结论:①△ECF的面积为![]() ;②△AEG的周长为8;③EG2=DG2+BE2;其中正确的是( )
;②△AEG的周长为8;③EG2=DG2+BE2;其中正确的是( )
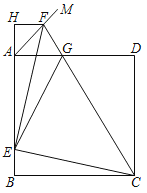
A.①②③B.①③C.①②D.②③
【答案】C
【解析】
先判断出∠H=90°,进而求出AH=HF=1=BE.进而判断出△EHF≌△CBE(SAS),得出EF=EC,∠HEF=∠BCE,判断出△CEF是等腰直角三角形,再用勾股定理求出EC2=17,即可得出①正确;先判断出四边形APFH是矩形,进而判断出矩形AHFP是正方形,得出AP=PH=AH=1,同理:四边形ABQP是矩形,得出PQ=4,BQ=1,FQ=5,CQ=3,再判断出△FPG∽△FQC,得出![]() ,求出PG=
,求出PG=![]() ,再根据勾股定理求得EG=
,再根据勾股定理求得EG=![]() ,即△AEG的周长为8,判断出②正确;先求出DG=
,即△AEG的周长为8,判断出②正确;先求出DG=![]() ,进而求出DG2+BE2=
,进而求出DG2+BE2=![]() ,在求出EG2=
,在求出EG2=![]() ≠
≠![]() ,判断出③错误,即可得出结论.
,判断出③错误,即可得出结论.
解:如图,在正方形ABCD中,AD∥BC,AB=BC=AD=4,∠B=∠BAD=90°,
∴∠HAD=90°,
∵HF∥AD,
∴∠H=90°,
∵∠HAF=90°﹣∠DAM=45°,
∴∠AFH=∠HAF.
∵AF=![]() ,
,
∴AH=HF=1=BE.
∴EH=AE+AH=AB﹣BE+AH=4=BC,
∴△EHF≌△CBE(SAS),
∴EF=EC,∠HEF=∠BCE,
∵∠BCE+∠BEC=90°,
∴HEF+∠BEC=90°,
∴∠FEC=90°,
∴△CEF是等腰直角三角形,
在Rt△CBE中,BE=1,BC=4,
∴EC2=BE2+BC2=17,
∴S△ECF=![]() EFEC=
EFEC=![]() EC2=
EC2=![]() ,故①正确:
,故①正确:
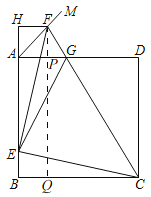
过点F作FQ⊥BC于Q,交AD于P,
∴∠APF=90°=∠H=∠HAD,
∴四边形APFH是矩形,
∵AH=HF,
∴矩形AHFP是正方形,
∴AP=PH=AH=1,
同理:四边形ABQP是矩形,
∴PQ=AB=4,BQ=AP1,FQ=FP+PQ=5,CQ=BC﹣BQ=3,
∵AD/span>∥BC,
∴△FPG∽△FQC,
∴![]() ,
,
∴![]() ,
,
∴PG=![]() ,
,
∴AG=AP+PG=![]() ,
,
在Rt△EAG中,根据勾股定理得,EG=![]() ,
,
∴△AEG的周长为AG+EG+AE=![]() =8,故②正确;
=8,故②正确;
∵AD=4,
∴DG=AD﹣AG=![]() ,
,
∴DG2+BE2=![]() +1=
+1=![]() ,
,
∵EG2=(![]() )2=
)2=![]() ≠
≠![]() ,
,
∴EG2≠DG2+BE2,故③错误,
∴正确的有①②,
故选:C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
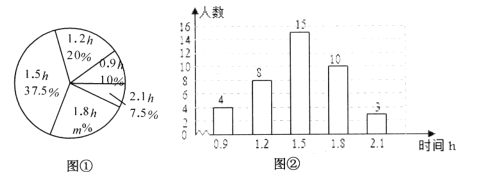
小学生10分钟应用题系列答案【题目】某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,

活动类型 | 频数(人数) | 频率 |
运动 | 20 | |
娱乐 | 40 | |
阅读 | ||
其他 | 0.1 |
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.