题目内容
【题目】类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，请看下面的案例．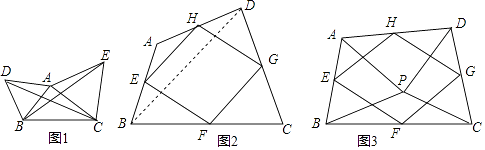
（1）如图1，已知△ABC，分别以AB、AC为边，在BC同侧作等边三角形ABD和等边三角形ACE，连接CD，BE．
通过证明△ ADC ≌△ ABE ，得到DC=BE；
（2）如图2，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点，顺次连接E、F、G、H，得到四边形EFGH，我们称四边形EFGH为四边形ABCD的中点四边形，连接BD，利用三角形中位线的性质，可得EH∥BD，EH= 
BD，同理可得FG∥BD，FG= BD，所以EH∥FG，EH=FG，所以四边形EFGH是平行四边形；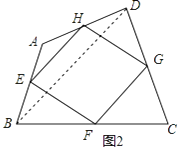
拓展应用
①如图3，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想四边形EFGH的形状，并证明；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，四边形EFGH的形状是 ．
【答案】
（1）解：如图1，
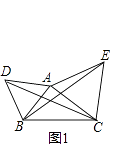
∵△ABD和△ACE都是等边三角形，
∴AD=AB，AC=AE，∠BAD=∠CAE=60°，
∴∠BAD+∠BAC=∠CAE+∠BAC，即∠DAC=∠BAE，
在△ADC和△ABE中
，
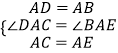∴△DAC≌△BAE（SAS），
∴DC=BE
（2）证明：四边形EFGH为菱形；理由如下：
连接AC、BD，如图3，
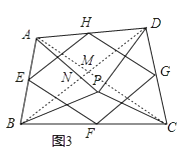
∵∠APB=∠CPD，
∴∠APB+APD=∠CPD+∠APD，即∠BPD=∠APC，
在△PBD和△APC中
，
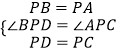∴△PBD≌△APC，
∴BD=AC，
∵HG= 
AC，HE= BD，
∴HG=HE，
∵四边形HEFG为平行四边形，
∴四边形EFGH为菱形
（3）正方形
【解析】解： （3）AC与BD相交于点M，BD交AP于N，如图3，
∵△PBD≌△APC，
∴∠PBD=∠PAC，
而∠ANM=∠BNP，
∴∠AMN=∠APB=90°，
∴AC⊥BD，
∵EH∥BD，HG∥AC，
∴EH⊥HG，
∴∠EHG=90°，
∵四边形EFGH为菱形，
∴四边形EFGH为正方形．
所以答案是：正方形．
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识，掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形，以及对正方形的判定方法的理解，了解先判定一个四边形是矩形，再判定出有一组邻边相等；先判定一个四边形是菱形，再判定出有一个角是直角．
