题目内容
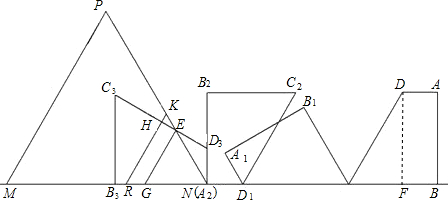
如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，BC=5，CD=6，∠DCB=60°，等边△PMN（N为固定点）的边长为x，边MN在直线BC上，NC=8．将直角梯形ABCD绕点C按逆时针方向旋转到①的位置，再绕点D1按逆时针方向旋转到②的位置，如此旋转下去．（1）将直角梯形按此方法旋转四次，如果等边△PMN的边长为x≥5+3
| 3 |
（2）将直角梯形按此方法旋转三次，如果梯形与等边三角形的重叠部分的面积是
19
| ||
| 2 |
（3）将直角梯形按此方法旋转三次，如果梯形与等边三角形的重叠部分的面积是梯形面积的一半，求等边△PMN的边长x．
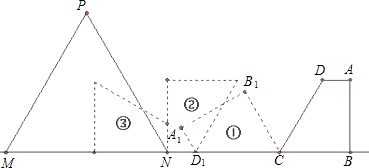
分析：（1）解本题要先判断出转2次后A点与N点的距离，根据题意，转2次的路程应该是CD+AD，如果过D作DF⊥BC，那么AD=BF=BC-CF，在直角三角形DCF中，CF=3，DF=3
，因此AD=2那么转动两次后的路程是6+2=8，因此转动两次后A，N两点是重合的，那么再看第三次和第四次转动的长度，即AB+BC的长，为5+3
，那么根据题意可知，梯形完全在等边三角形内，因此重合部分的面积其实就是梯形的面积．根据梯形的面积计算方法和已知的数据即可求出梯形的面积．
（2）本题的关键是要判断出旋转3次后哪些是重合部分，如果设旋转3次后PN与DC交于N，那么先要求出四边形CBNK的面积是多少，如果四边形的面积大于
，则说明四边形CBNK只有部分在等边三角形内，如果四边形的面积等于
，就说明四边形CBNK全部在等边三角形内，这点对判断等边三角形的边长的取值范围至关重要．那么先求四边形CBNK的面积．由于四边形的面积=梯形的面积-三角形NKD的面积，那么关键是求出三角形NDK的面积，已知了三角形的底边ND的长，可过K作ND边上的高KH，那么直角三角形NKH中，∠KNH=30°，∠NDK=120°，由此可得出∠HKD=∠HDK=30°，KD=AD=2，那么可求出DH，KH的长，也就求出了三角形NDK的面积，进而可得出四边形CBNK的面积为
，由此可得出四边形CBNK全部在等边三角形内，那么可通过计算此时等边三角形的边长最小的情况来得出等边三角形的边长的取值范围，过C作PM的平行线EG，然后在上下两个直角三角形中分别求出CE和CG，那么EG就是等边三角形边长的最小值，由此可得出等边三角形的边长的取值范围．
（3）本题要先判断等边三角形边长的大致范围，因为这影响到重合部分的面积的计算方法，可过B作PM的平行线BK，过E作PM的平行线EG交CD于H，那么要先判断四边形BHEN的面积是否是梯形面积的一半，也就是求三角形BHC和NDE的面积和是否为梯形面积的一半，我们可求的两三角形的面积和小于梯形的面积的一半，那么等边三角形的PM边必在BK与GE中间，那么我们设这边为RK还是交CD于H，那么可先求出三角形GEN的面积，然后可根据GEN与RNH相似，用相似比表示出三角形RNH的面积，然后再求出三角形HKE的面积，这样四边形RHEN的面积=三角形RNH的面积-三角形HKE的面积=梯形的面积的一半，由此可得出关于x的方程，求出x的值即可．
| 3 |
| 3 |
（2）本题的关键是要判断出旋转3次后哪些是重合部分，如果设旋转3次后PN与DC交于N，那么先要求出四边形CBNK的面积是多少，如果四边形的面积大于
19
| ||
| 2 |
19
| ||
| 2 |
19
| ||
| 2 |
（3）本题要先判断等边三角形边长的大致范围，因为这影响到重合部分的面积的计算方法，可过B作PM的平行线BK，过E作PM的平行线EG交CD于H，那么要先判断四边形BHEN的面积是否是梯形面积的一半，也就是求三角形BHC和NDE的面积和是否为梯形面积的一半，我们可求的两三角形的面积和小于梯形的面积的一半，那么等边三角形的PM边必在BK与GE中间，那么我们设这边为RK还是交CD于H，那么可先求出三角形GEN的面积，然后可根据GEN与RNH相似，用相似比表示出三角形RNH的面积，然后再求出三角形HKE的面积，这样四边形RHEN的面积=三角形RNH的面积-三角形HKE的面积=梯形的面积的一半，由此可得出关于x的方程，求出x的值即可．
解答：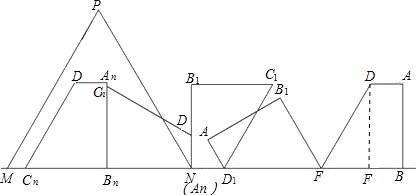
解：
（1）过点D作DF⊥BC，垂足为F，
∵CD=6，∠DCB=60°，
∴∠CDF=30°，
∴CF=
DC=3，DF=3
，
∴BF=BC-CF=2，
又∵梯形ABCD为直角梯形，
∴∠A=∠B=90°而∠DFB=90°，
∴四边形ABFD为矩形，
∴AD=BF=2，
∴A2D1+D1C=2+6=8，
又∵NC=8，
∴点N与A2重合，
∵C4N=B3C4+B3N=5+3
，
又∵MN＞5+3
，
∴直角梯形与等边三角形的重叠部分即为整个直角梯形，
∴S重叠部分=
(2+5)3
=
．
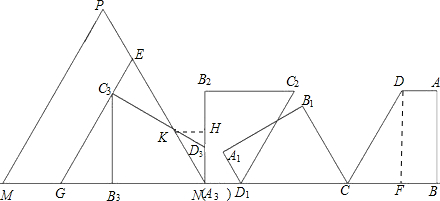
（2）过点C3作GE∥MP交MN于点G，交NP于占E，
则△GNE为等边三角形，
过点K作KH⊥B2N，垂足为H，
在Rt△NKH中∠KNH=30°，∠ND3K=120°，
∴∠KNH=∠NKD3，
∴ND3=D3K=2，
∴D3H=1，KH=
，
∴S△D3KH=
×1×
=
，
而S梯形=
，
∴S梯形-S△ND3K=
-
=
=重叠部分面积，
在Rt△GC3B3中，∠GC3B3=30°，C3B3=5，
∴GC3=
=
，
C3K=C3D3-D3K=6-2=4，
C3E=C3Ktan30°=4×
=
，
∴GE=GC3+C3E=
+
=
，
∴等边△PMN的边长x的范围为：x≥
，
（3）如图：GE∥B3K∥PM，
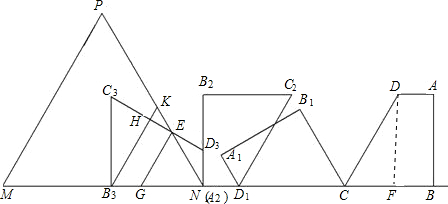
Rt△B3C3H中，B3C3=5，∠C3=30°，
∴Rt△B3C3H的面积为：
，
∴Rt△B3C3H的面积+△D3NE的面积=
+
=
＜
（梯形面积的一半），
等边三角形的一边RK应落在GE与B3K之间，如图所示，
等边△GNE的边长为2
，面积为3
，
∵GE∥RK，
∴△GNE∽△RNK，
∴S△GNE：S△RNK=（NE：NK）2，
设KE=x，则S△GNE：S△RNK=（
）2，
而四边形RNEH的面积为梯形的面积的一半，即
，
在△HEK中，KE=x，∠KEH=30°，
∴S△KEH=
，
∴S△NRK=
+
+
，
∴（
）2=
，
∴x=
，
∴x=-4
+
（负值舍去），
RN=NE+EK=2
+（-4
+
）=
-2
，
即此时等边三角形的边长为：
-2
．
解：
（1）过点D作DF⊥BC，垂足为F，
∵CD=6，∠DCB=60°，
∴∠CDF=30°，
∴CF=
| 1 |
| 2 |
| 3 |
∴BF=BC-CF=2，
又∵梯形ABCD为直角梯形，
∴∠A=∠B=90°而∠DFB=90°，
∴四边形ABFD为矩形，
∴AD=BF=2，
∴A2D1+D1C=2+6=8，
又∵NC=8，
∴点N与A2重合，
∵C4N=B3C4+B3N=5+3
| 3 |
又∵MN＞5+3
| 3 |
∴直角梯形与等边三角形的重叠部分即为整个直角梯形，
∴S重叠部分=
| 1 |
| 2 |
| 3 |
21
| ||
| 2 |
（2）过点C3作GE∥MP交MN于点G，交NP于占E，
则△GNE为等边三角形，
过点K作KH⊥B2N，垂足为H，
在Rt△NKH中∠KNH=30°，∠ND3K=120°，
∴∠KNH=∠NKD3，
∴ND3=D3K=2，
∴D3H=1，KH=
| 3 |
∴S△D3KH=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
而S梯形=
21
| ||
| 2 |
∴S梯形-S△ND3K=
21
| ||
| 2 |
| ||
| 2 |
19
| ||
| 2 |
在Rt△GC3B3中，∠GC3B3=30°，C3B3=5，
∴GC3=
| BC |
| cos30° |
10
| ||
| 3 |
C3K=C3D3-D3K=6-2=4，
C3E=C3Ktan30°=4×
| ||
| 3 |
4
| ||
| 3 |
∴GE=GC3+C3E=
10
| ||
| 3 |
4
| ||
| 3 |
14
| ||
| 3 |
∴等边△PMN的边长x的范围为：x≥
14
| ||
| 3 |
（3）如图：GE∥B3K∥PM，
Rt△B3C3H中，B3C3=5，∠C3=30°，
∴Rt△B3C3H的面积为：
25
| ||
| 8 |
∴Rt△B3C3H的面积+△D3NE的面积=
25
| ||
| 8 |
| 3 |
33
| ||
| 8 |
21
| ||
| 4 |
等边三角形的一边RK应落在GE与B3K之间，如图所示，
等边△GNE的边长为2
| 3 |
| 3 |
∵GE∥RK，
∴△GNE∽△RNK，
∴S△GNE：S△RNK=（NE：NK）2，
设KE=x，则S△GNE：S△RNK=（
2
| ||
x+2
|
而四边形RNEH的面积为梯形的面积的一半，即
21
| ||
| 4 |
在△HEK中，KE=x，∠KEH=30°，
∴S△KEH=
| ||
| 8 |
∴S△NRK=
21
| ||
| 4 |
21
| ||
| 4 |
| ||
| 8 |
∴（
2
| ||
x+2
|
3
| ||||||||
|
∴x=
-8±2
| ||
| 2 |
∴x=-4
| 3 |
| 66 |
RN=NE+EK=2
| 3 |
| 3 |
| 66 |
| 66 |
| 3 |
即此时等边三角形的边长为：
| 66 |
| 3 |
点评：本题主要考查了旋转的性质，解直角三角形的应用以及相似三角形的性质等知识点，根据题目给出的条件先判断出重合部分的形状，进而选择合适的面积计算方法是解题的关键．
练习册系列答案
相关题目
20、如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点．将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中阴影所示）．若∠A=130°，AB=4cm，则梯形ABCD的高CD≈
如图，在直角梯形ABCD中，AB∥DC，∠D=90°，AC⊥BC，AB=10cm，BC=6cm，F点以2cm/秒的速度在线段AB上由A向B匀速运动，E点同时以1cm/秒的速度在线段BC上由B向C匀速运动，设运动时间为t秒（0＜t＜5）．
（1998•大连）如图，在直角梯形ABCD中．AD∥BC，DC⊥BC，且BC=3AD．以梯形的高AE为直径的⊙O交AB于点F，交CD于点G、H．过点F引⊙O的切线交BC于点N．
BC上的动点，点G在AB上，且四边形AEFG是矩形．设FG=x，矩形AEFG的面积为y．