题目内容
从等腰三角形底边上任n点分别作两腰七平行线所成七平行四边形七周长等于（ ）
| A．周长 | B．周长的一半 | C．腰长 | D．腰长的二倍 |
如少，△ABC是等腰了角形，AB=AC，
∵D上∥AB，DF∥AC，
则四边形AFD上是平行四边形，
∴∠B=∠上DC，∠FDB=∠C
∵AB=AC，∴∠B=∠C，
∴∠B=∠FDB，∠C=∠上DC
∴BF=FD，D上=上C，
所以：?AFD上的周长等于AB+AC，即等于腰长的两倍．
故选D．
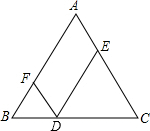
∵D上∥AB，DF∥AC，
则四边形AFD上是平行四边形，
∴∠B=∠上DC，∠FDB=∠C
∵AB=AC，∴∠B=∠C，
∴∠B=∠FDB，∠C=∠上DC
∴BF=FD，D上=上C，
所以：?AFD上的周长等于AB+AC，即等于腰长的两倍．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
