��Ŀ����
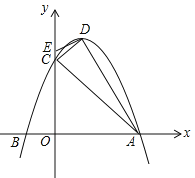
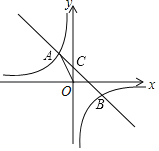
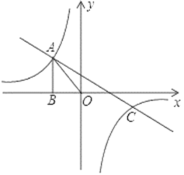
����Ŀ����ͼ����֪����������y1��![]() ��һ�κ���y2��k2x+b��ͼ���ཻ�ڵ�A��C���㣬���е�A�ĺ�����Ϊ��2����C��������Ϊ��1������A��AB��x���ڵ�B����AOB�����Ϊ2��
��һ�κ���y2��k2x+b��ͼ���ཻ�ڵ�A��C���㣬���е�A�ĺ�����Ϊ��2����C��������Ϊ��1������A��AB��x���ڵ�B����AOB�����Ϊ2��
��1������������һ�κ����Ľ���ʽ��
��2������ͼ��ֱ�ӻش𣺵�xȡ��ֵʱ��һ�κ������ڷ�����������ֵ��
��3����A�����x��ĶԳƵ�A���ڶ��κ���y3����x2+mx+n��ͼ���ϣ����ж϶��κ���y4��x2+mx��n��3��x��Ľ����������˵�����ɣ�
���𰸡���1��![]() ��
��![]() ����2��x����2��0��x��4����3���������㣬������
����2��x����2��0��x��4����3���������㣬������
��������
(1)���ݷ���������![]() �ļ������壬�õ�
�ļ������壬�õ�![]() =4���̶��õ���
=4���̶��õ���![]() =-4�������A��C�������꣬����һ�κ�������ʽ�ù���
=-4�������A��C�������꣬����һ�κ�������ʽ�ù���![]() ��b�Ķ�Ԫһ�η����飬���һ�κ�������ʽ��
��b�Ķ�Ԫһ�η����飬���һ�κ�������ʽ��
(2)�۲�ͼ��![]() ��
��![]() ������ʾ
������ʾ![]() ��ͼ��λ��
��ͼ��λ��![]() ��ͼ���Ϸ���ֱ���ҳ���Ӧ��x��ȡֵ��Χ��
��ͼ���Ϸ���ֱ���ҳ���Ӧ��x��ȡֵ��Χ��
(3)������ɵõ�n=2m+2���ٸ��ݶ��κ���ͼ����x�ύ��������Ӧ��һԪ���η��̸�������йأ����![]() ��ֵ�����жϣ�
��ֵ�����жϣ�
(1)��S��AOB=2��
��![]() =4��
=4��
��![]() ��ͼ��λ�ڵڶ��������ޣ�
��ͼ��λ�ڵڶ��������ޣ�
��![]() ��
��
��![]() ��
��
��A(��2��2)��C(4����1)��
������ã�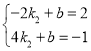 ��
��
���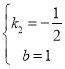 ��
��
��![]() ��
��
(2)�۲�ͼ��ã�
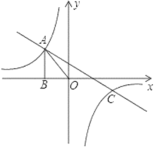
��x����2��0��x��4ʱ��һ�κ�����ͼ���ڷ���������ͼ����Ϸ���
�൱x����2��0��x��4ʱ��y2��y1��
(3)�� A(��2��2)����x��ĶԳƵ�A��������Ϊ(��2����2)��
�������⣬��A�� (��2����2)��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ����
����![]() ��
��
��![]()
![]()
![]()
![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
�����x��һԪ���η���![]() ����������ȵ�ʵ������
����������ȵ�ʵ������
�����κ���![]() ��ͼ����x�����������㣮
��ͼ����x�����������㣮

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
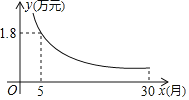
��У���˿��ֿ���ϵ�д�����Ŀ��Ѵ�ڵ�����ɽ�鱩�����±���¼��ijˮ��![]() ��ˮλ�ı仯���������
��ˮλ�ı仯���������![]() ��ʾʱ��(��λ��
��ʾʱ��(��λ��![]() )��
)��![]() ��ʾˮλ�߶�(��λ��
��ʾˮλ�߶�(��λ��![]() )����
)����![]() ʱ���ﵽ����ˮλ����ʼ��բ��ˮ��
ʱ���ﵽ����ˮλ����ʼ��բ��ˮ��
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |

(1)�ڸ�����ƽ��ֱ������ϵ�У����ݱ����е����������Ӧ�ĵ㣮
(2)��ֱ������բ��ˮǰ�ͷ�ˮ������ϱ������ݵĺ�������ʽ��
(3)�ݹ��ƣ���բ��ˮ��ˮλ�����ֱ仯���ɻ������һ��ʱ�䣬Ԥ���ʱˮλ�ﵽ![]() ��
��