Question

【题目】如图,反比例函数的图象与直线 (a≠0)交于A,B两点,点A的横坐标为3．（1）则a的值为________；（2）若平行于的直线经过点A,与反比例函数的图象交另一点C,则△ABC的面积为____________．

Answer 1

【答案】 8

【解析】（1）根据反比例函数图象上点的坐标特征结合点A的横坐标即可得出点A的坐标，再利用一次函数图象上点的坐标特征即可求出a的值；

（2）过点 A 作AD⊥x轴交AB于点D，设直线AC的解析式为y=-x+b，根据A点的坐标即可求出直线AC的解析式，联立直线AC与反比例函数解析式成方程组即可求出点C的坐标，再利用一次函数图象上点的坐标特征可求出点D的坐标，结合三角形的面积即可求出△ABC的面积，此题得解.

解：（1）∵点AB的横坐标为3且点A在反比例函数y=的图象上，

∴点A的坐标为（3，1）,

又∵点A在直线y=ax上，

∴1=3a，解得：a=,

故答案为： .

（2）过点 A 作AD⊥x轴交AB于点D，如图所示.

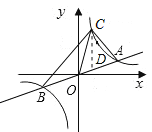
设直线AC的解析式为y=-x+b，

∵点A在直线AC上，

∴1=-3+b，解得：b=4，

∴直线AC的解析式为y=-x+4.

联立直线AC与反比例函数解析式成方程组，

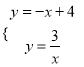解得： 和，

∴点C的坐标为（1，3），

当x=1时，y=x=，

∴点D的坐标为（1， ）.

∵反比例函数y=的图象与直线y=ax（a≠0）交于A、B两点，点A的坐标为（3，1）,

∴点B的坐标为（-3，-1）.

∴S△ABC=CD×（xA-xB）=×（3-）×[3-(-3)]=8.

故答案为：8.

“点睛”本题考查了反比例函数与一次函数的交点问题、一次函数图象上的坐标特征以及三角形的面积，解题的关键是：（1）根据反比例函数图象上点的坐标特征找出点A的坐标；（2）根据点A的坐标求出直线AC的解析式.