题目内容
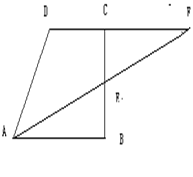
如图,在等腰梯形ABCD中,AB∥DC,AD=BC=5cm,AB=12cm,CD=6cm,点Q从C开始沿CD边向D移动,速度是每秒1厘米,点P从A开始沿AB向B移动,速度是点Q速度的a倍,如果点P,Q分别从A,C同时出发,当其中一点到达终点时运动停 止.设运动时间为t秒.已知当t=
止.设运动时间为t秒.已知当t= 时,四边形APQD是平行四边形.
时,四边形APQD是平行四边形.

(1)求a的值;
(2 )线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说
)线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说 明理由;
明理由;
(3)若在某一时刻点P恰好在DQ的垂直平分线上,求此时t的值.
 止.设运动时间为t秒.已知当t=
止.设运动时间为t秒.已知当t= 时,四边形APQD是平行四边形.
时,四边形APQD是平行四边形.
(1)求a的值;
(2
 )线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说
)线段PQ是否可能平分对角线BD?若能,求t的值,若不能,请说 明理由;
明理由;(3)若在某一时刻点P恰好在DQ的垂直平分线上,求此时t的值.
(1)a=3
(2)t=3
(3)

解:(1)∵四边形APQD是平行四边形
∴6- =
= ,即:
,即: …………(2分)
…………(2分)
(2)若线段PQ平分对角线BD,即DO=BO
则△DOQ≌△BOP …………(4分)
∴DQ=BP
即:6-t="12-3t " 解得t="3 " …………(5分)
(3)分别过点C、D作CN⊥AB,DM⊥AB,交AB于点M、N

可得:四边形DNPM是矩形,△DAM≌△CBN
∴AM= ="3 " …………(6分)
="3 " …………(6分)
∵点P恰好在DQ的垂直平分线EP上
∴PD=PQ,DM= DQ,四边形DNPM是矩形
DQ,四边形DNPM是矩形
∴DM=NP
即: ,解得:
,解得: …………(8分)
…………(8分)
∴6-
 =
= ,即:
,即: …………(2分)
…………(2分)(2)若线段PQ平分对角线BD,即DO=BO
则△DOQ≌△BOP …………(4分)
∴DQ=BP
即:6-t="12-3t " 解得t="3 " …………(5分)
(3)分别过点C、D作CN⊥AB,DM⊥AB,交AB于点M、N

可得:四边形DNPM是矩形,△DAM≌△CBN
∴AM=
 ="3 " …………(6分)
="3 " …………(6分)∵点P恰好在DQ的垂直平分线EP上
∴PD=PQ,DM=
 DQ,四边形DNPM是矩形
DQ,四边形DNPM是矩形∴DM=NP
即:
 ,解得:
,解得: …………(8分)
…………(8分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
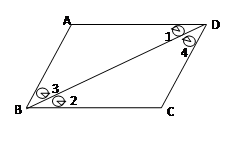
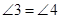 .
.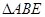 ≌
≌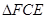
 中,
中, ,
, ,
, .
.
 、
、 表示
表示 、
、 ;(直接写出答案)
;(直接写出答案) 、
、 方向上的分向量.
方向上的分向量.
 中,已知对角线
中,已知对角线 和
和 相交于点
相交于点 ,
, 的周长为15㎝,
的周长为15㎝, ㎝,则
㎝,则 ㎝
㎝
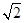 ∶1
∶1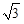 ∶1
∶1