题目内容
已知第1个数是14，第2个数是17，第3个数是21，则第4个数是________，第10个数是________，第n个数是________．
26 77 
n2+
n+12
分析：根据第1个数是14，第2个数是14+3=17，第3个数是14+3+4=21，得出第4个数是14+3+4+5，第10个数是14+3+4+5+6+7+8+9+10+11，根据规律即可得出第n个数是n2+n+12．
解答：因为第1个数是14，
第2个数是14+3=17，
第3个数是14+3+4=21，
所以第4个数是14+3+4+5=26，
第10个数是14+3+4+5+6+7+8+9+10+11=77，
第n个数是14+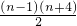
=n2+n+12；
故答案为：26，77，n2+n+12；
点评：此题考查了数字的变化类，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是本题的关键．
n2+n+12分析：根据第1个数是14，第2个数是14+3=17，第3个数是14+3+4=21，得出第4个数是14+3+4+5，第10个数是14+3+4+5+6+7+8+9+10+11，根据规律即可得出第n个数是
n2+n+12．解答：因为第1个数是14，
第2个数是14+3=17，
第3个数是14+3+4=21，
所以第4个数是14+3+4+5=26，
第10个数是14+3+4+5+6+7+8+9+10+11=77，
第n个数是14+
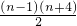=n2+n+12；故答案为：26，77，
n2+n+12；点评：此题考查了数字的变化类，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是本题的关键．
练习册系列答案
名校课堂系列答案
相关题目