��Ŀ����
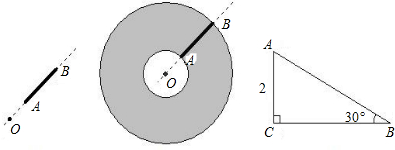
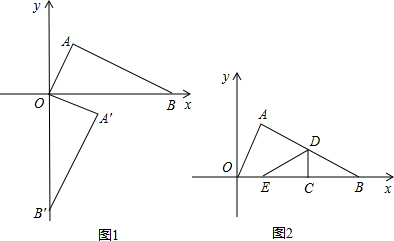
��ͼ1����Rt��A��OB���У���B��A��0=90�㣬A�䣬B�����������ֱ�Ϊ��2��-1���ͣ�0��-5������A��0B���Ƶ�O��ʱ�뷽����ת90�㣬ʹOB������x���������ϣ��á�AOB����A��Ķ�Ӧ����A����B���Ķ�Ӧ����B����1��д��A��B��������꣬����ֱ��AB�Ľ���ʽ��
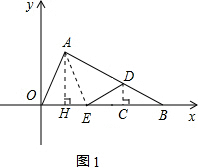
��2����ͼ2������A0B�ش�ֱ��x����߶�CD�۵�������C��x���ϣ��Ҳ����B�غϣ���D���߶�AB�ϣ���ʹ��B����x���ϣ���Ӧ��Ϊ��E�����C������Ϊ��x��0����
�ٵ�xΪ��ֵʱ���߶�DEƽ�֡�AOB�������
���Ƿ���������ĵ�ʹ�á�AEDΪֱ�������Σ������ڣ������C�����ꣻ�������ڣ���˵�����ɣ�
�����CDE���AOB�ص����ֵ����ΪS��ֱ��д��S���C�ĺ�����x֮��ĺ�
 ����ϵʽ�������Ա���x��ȡֵ��Χ����
����ϵʽ�������Ա���x��ȡֵ��Χ����
��������1��������ת�����ʿ�֪��A��ĺ�����ʵ����A��������꣬A���������ľ���ֵʵ����A������꣬�ɴ˿ɵó�A������꣬ͬ�������B������꣮��֪��A��B�����꣬���ô���ϵ�������ֱ��AB�Ľ���ʽ��
��2���ٵ�E����O�غ�ʱ�����ѵó���EDB�������
��AOB���������˵��߶�DEƽ�֡�AOB�����ʱ��E��O���Ҳ࣮����x��ʾ��BC��CD��ֵ�������ɵ������BDE�������Ȼ����������Ϊ��AOB�����һ��ɵó�һ������x�ķ��̣��ݴ˿����x��ֵ��
�ڱ���Ҫ������������ۣ�
һ������ADE=90��ʱ����EDB=90�㣬��Ȼ��������
��������EAD=90��ʱ��E��O�غϣ���ôBE=BO���ݴ˿����x��ֵ��
��������AED=90��ʱ���ɹ�A��x��Ĵ��ߣ�ͨ���������������������x��ֵ��
�۱���Ҫ������������ۣ�
һ����
��x��5ʱ��E�ڡ�AOB�ڣ��غϲ��ֵ�������ǡ�CDE�������
����2��x��
ʱ��E�ڡ�AOB�ⲿ���غϲ����Ǹ���������ı��Σ���DE��OA����P����ô�غϲ��ֵ�������á�CDE�������ȥ��EOP���������ã�
�������������������ͬx��ȡֵ��Χ��S��x�ĺ�����ϵʽ��
��2���ٵ�E����O�غ�ʱ�����ѵó���EDB�������
| 1 |
| 2 |
�ڱ���Ҫ������������ۣ�
һ������ADE=90��ʱ����EDB=90�㣬��Ȼ��������
��������EAD=90��ʱ��E��O�غϣ���ôBE=BO���ݴ˿����x��ֵ��
��������AED=90��ʱ���ɹ�A��x��Ĵ��ߣ�ͨ���������������������x��ֵ��
�۱���Ҫ������������ۣ�
һ����
| 5 |
| 2 |
����2��x��
| 5 |
| 2 |
�������������������ͬx��ȡֵ��Χ��S��x�ĺ�����ϵʽ��
����⣺��1��A��1��2����B��5��0����
��ֱ��AB�Ľ���ʽΪy=kx+b�����У�
��
��ã�
��
��ֱ��AB�Ľ���ʽΪy=-
x+
��
��2���ٵ�x=
ʱ��CD=y=
=
��S��DEB=
��5��
=
��3��
���E��O���ұߣ�
�����⣬�ã�S��DEB=
��2��5-x����
=
��x=5+
����ȥ����
��x=5-
��
�ڵ���ADE=90��ʱ���á�DBE=��DEB=45�㣬��ȥ��
����EAD=90��ʱ����E���O�غϣ���x=
��
����AED=90��ʱ����AH��OB��H��֤����AHE�ס�DCE���ɵ�HE=1��
��OE=2��
��2+2��5-x��=5��x=
��
�۵�
��x��5ʱ��S=
����5-x����
=
��x-5��2��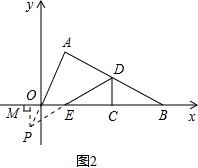
��2��x��
ʱ����DE��OA����P����PM��OB��M����PM=h����OM=
��EM=2h��OE=5-2x��
��5-2x+
=2h��h=
��5-2x����
��S=
����5-x����
-
����5-2x����
��5-2x��=-
x2+
x-
��
��ֱ��AB�Ľ���ʽΪy=kx+b�����У�
|
��ã�
|
��ֱ��AB�Ľ���ʽΪy=-
| 1 |
| 2 |
| 5 |
| 2 |
��2���ٵ�x=
| 5 |
| 2 |
| 5-x |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
| 25 |
| 8 |
���E��O���ұߣ�
�����⣬�ã�S��DEB=
| 1 |
| 2 |
| 5-x |
| 2 |
| 5 |
| 2 |
| 5 |
��x=5-
| 5 |

�ڵ���ADE=90��ʱ���á�DBE=��DEB=45�㣬��ȥ��
����EAD=90��ʱ����E���O�غϣ���x=
| 5 |
| 2 |
����AED=90��ʱ����AH��OB��H��֤����AHE�ס�DCE���ɵ�HE=1��
��OE=2��
��2+2��5-x��=5��x=
| 7 |
| 2 |
�۵�
| 5 |
| 2 |
| 1 |
| 2 |
| 5-x |
| 2 |
| 1 |
| 4 |

��2��x��
| 5 |
| 2 |
| h |
| 2 |
��5-2x+
| h |
| 2 |
| 2 |
| 3 |
��S=
| 1 |
| 2 |
| 5-x |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 13 |
| 12 |
| 25 |
| 6 |
| 25 |
| 12 |
������������Ҫ�����˶��κ�������ʽ��ȷ����ͼ�εķ��۱任��ͼ�ε������֪ʶ���ۺ�Ӧ��֪ʶ����������������

��ϰ��ϵ�д�
 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
�����Ŀ
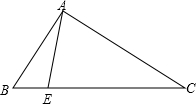 ��ͼ��֪��Rt��ABC�У���BAC=90�㣬E��б��BC�ϣ�CE=CA����֤����BAE=
��ͼ��֪��Rt��ABC�У���BAC=90�㣬E��б��BC�ϣ�CE=CA����֤����BAE=