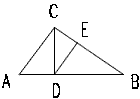
题目内容
 如图已知在Rt△ABC中,∠BAC=90°,E在斜边BC上,CE=CA,求证:∠BAE=
如图已知在Rt△ABC中,∠BAC=90°,E在斜边BC上,CE=CA,求证:∠BAE=| 1 | 2 |
分析:根据直角三角形性质可证∠BAE=90°-∠CAE,根据等腰三角形的性质可证∠CAE=
(180°-∠ACB),将后式代入前式即可证明∠BAE=
∠ACB.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵在Rt△ABC中,∠BAC=90°,
∴∠BAE=90°-∠CAE,
∵CE=CA,
∴∠CAE=
(180°-∠ACB),
∴∠BAE=90°-∠CAE=90°-
(180°-∠ACB)=
∠ACB.
∴∠BAE=90°-∠CAE,
∵CE=CA,
∴∠CAE=
| 1 |
| 2 |
∴∠BAE=90°-∠CAE=90°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查学生对直角三角形性质和等腰三角形的性质的理解和掌握,此题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


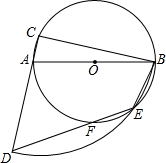 (2013•武汉模拟)如图,已知在Rt△ABC中,∠ACB=90°,BC>AC,⊙O为△ABC的外接圆,以点C为圆心,BC长为半径作弧交CA的延长线于点D,交⊙O于点E,连接BE、DE.
(2013•武汉模拟)如图,已知在Rt△ABC中,∠ACB=90°,BC>AC,⊙O为△ABC的外接圆,以点C为圆心,BC长为半径作弧交CA的延长线于点D,交⊙O于点E,连接BE、DE. (2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )
(2012•咸丰县二模)如图,已知在Rt△ABC中,∠ACB=90°,AB=10,分别以AC、BC为直经作半圆,面积分别记为S1、S2,则S1+S2的值等于( )