Question

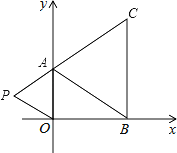
【题目】如图，Rt△ABC中，AB=AC=8，BO=AB，点M为BC边上一动点，将线段OM绕点O按逆时针方向旋转90°至ON，连接AN、CN，则△CAN周长的最小值为________.

Answer 1

【答案】8+4.

【解析】

过点O作OB′⊥AB于点O，交BC于点B′，连接B′N并延长交AB于点E，易证△BOM≌△B′ON（SAS），∴点N始终在经过点B′且与BC垂直的射线上，因为△CAN周长=CA+AN+CN=8+ AN+CN，所以AN+CN值最小时，周长最小，属于最短路径问题，关键找点C关于B′E的对称点C′，连接A C′，与B′E的交点N′即为周长最小时的点N，此时AN+CN=AC′，求出AC′的值即可求出周长最小值.

解：过点O作OB′⊥AB于点O，交BC于点B′，连接B′N并延长交AB于点E，∵Rt△ABC中，AB=AC，

∴∠OBB′=45°=∠OB′B，OB =OB′

又∵∠BOB′=∠MON=90°

∴∠BOM=∠B′ON

∴△BOM≌△B′ON（SAS）

∴∠OBB′=45°=∠OB′N，即∠BB′N=90°，OB′= OB=2，BB′=2 ，

∴点N始终在经过点B′且与BC垂直的射线上，

易证△BB′E是等腰直角三角形，BE=4，即BE=AE，

∵△CAN周长=CA+AN+CN=8+ AN+CN

∴AN+CN值最小时，周长最小，属于最短路径问题，

∴找点C关于B′E的对称点C′，连接A C′，与B′E的交点N′即为周长最小时的点N，此时AN+CN=AC′，

等腰直角三角形△BB′E中， 由勾股定理得BB′=2，

等腰直角三角形△ABC中， BC=8 由三线合一得：BD=DC=AD=BC=4，

∴B′C=BC- BB′=8-2=6，由对称性得：B′C=B′C′=6，

∴C′D=12-4=8，

即：Rt△AC′D中，A C′= ==4

∴△CAN周长的最小值=8+ AN+CN=8+4.