题目内容
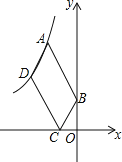
【题目】如图,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD. 
(1)求证:△COD是等边三角形.
(2)当α=150°时,试判断△AOD的形状.
(3)探究:当α为多少度时,△AOD是等腰三角形?
【答案】
(1)证明:由旋转的性质知△ADC≌△BOC,
∴DC=OC.
又∵∠DCO=60°,∴△COD是等边三角形
(2)解:∵由旋转的性质知△ADC≌△BOC,
∴α=∠ADC=150°,
∵△COD是等边三角形.
∴∠ODC=60°,
∴∠ADO=90°.
∴△AOD是直角三角形.
(3)解:∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∠DAO=180°-(190°-α)-(α-60°)=50°.
若∠ADO=∠AOD,即α-60°=190°-α,∴α=125°;
若∠ADO=∠DAO,即α-60°=50°,∴α=110°;
若∠AOD=∠DAO,即190°-α=50°.∴α=140°.
综上所述,当α=125°或110°或140°时,△AOD是等腰三角形.
【解析】(1)根据旋转的性质得出DC=OC及∠DCO=60°,再根据有一个角是60°的等腰三角形是等边三角形,即可证得结论。
(2)根据旋转的性质得到△ADC≌△BOC,再根据全等三角形的性质求出∠ADC的度数,再根据等边三角形的性质求出∠ODC的度数,然后根据∠ADO=∠ADC-∠ODC,求出∠ADO的度数,就可判断△AOD的形状。
(3)根据旋转的性质分别用含α的式子表示出∠AOD,∠ADO,∠DAO的度数,再分三种情况讨论:∠ADO=∠AOD;∠ADO=∠DAO;∠AOD=∠DAO,计算即可求出满足条件的α的值。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目