题目内容
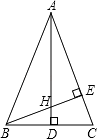
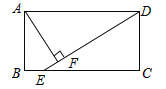
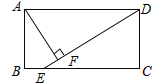
【题目】如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）
A．△AFD≌△DCE B．AF=
AD C．AB=AF D．BE=AD﹣DF
【答案】B．
【解析】
试题分析：A．由矩形ABCD，AF⊥DE可得∠C=∠AFD=90°，AD∥BC，∴∠ADF=∠DEC．
又∵DE=AD，∴△AFD≌△DCE（AAS），故（A）正确；
B．∵∠ADF不一定等于30°，∴直角三角形ADF中，AF不一定等于AD的一半，故（B）错误；
C．由△AFD≌△DCE，可得AF=CD，由矩形ABCD，可得AB=CD，∴AB=AF，故（C）正确；
D．由△AFD≌△DCE，可得CE=DF，由矩形ABCD，可得BC=AD，又∵BE=BC﹣EC，∴BE=AD﹣DF，故（D）正确；
故选B．
练习册系列答案
相关题目
