题目内容
【题目】某县区大力发展甜瓜产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些甜瓜运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的甜瓜为x吨,A、B两地运往两仓库的甜瓜运输费用分别为![]() .
.
(1)分别求出![]() 与x之间的函数关系式;
与x之间的函数关系式;
(2)试讨论A、B两地中,哪个的运费较少;
(3)考虑B地的经济承受能力,B地的甜瓜运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
【答案】(1)![]() ,
, ![]() ;
;
(2)x<40时,B地的运费较少;x=40时,两地的运费一样多;x>40时,A地的运费较少;
(3)当A地运往甲、乙两仓库分别为50吨、150吨;B地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之和最少,最少是9580元。
【解析】试题分析:(1)由运费=数量×单价就可以得出出yA、yB与x之间的函数关系式;
(2)当yA>yB,yA=yB或yA<yB时求出x的值就可以得出结论;
(3)设两地运费之和为W元,表示出W与x的关系式,由B地的猕猴桃运费不得超过4830元建立不等式求出x的取值范围就可以得出结论.
解:(1)![]()
![]()
(2)∵![]()
∴当![]() 时,B地的运费较少;
时,B地的运费较少;
当![]() 即x=40时,两地的运费一样多;
即x=40时,两地的运费一样多;
当![]() 即x>40时,A地的运费较少;
即x>40时,A地的运费较少;
(3)设两地运费之和为y元,则
![]()
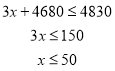
∵y随x的增大而减小,x最大为50
∴![]()
∴在此情况下,当A地运往甲、乙两仓库分别为50吨、150吨;B地运往甲、乙两仓库分别为190吨、110吨时,才能使两地运费之和最少,最少是9580元

【题目】体育课上,对初三(1)的学生进行了仰卧起坐的测试,以能做24个为标准,超过次数用正数来表示,不足的次数用负数来表示,其中10名女学生成绩如下:
5 | -2 | -1 | 3 | 0 | 10 | 0 | 7 | -5 | -1 |
(1)这10名女生的达标率为多少?
(2)她们共做了多少个仰卧起坐?