题目内容
如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0),将矩形OABC绕点O按顺时针方向旋转1800,得到矩形OEFG,顺次连接AC、CE、EG、GA.
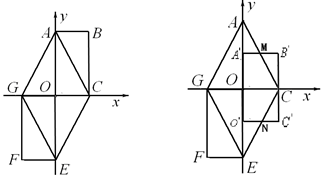
(1)请直接写出点F的坐标;
(2)试判断四边形ACEG的形状,并说明理由;
(3)将矩形OABC沿y轴向下平移m个单位(0<m<4),设平移过程中矩形与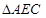 重叠部分面积为
重叠部分面积为 ,当
,当 :
: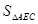 =11:16时,求m的值.
=11:16时,求m的值.
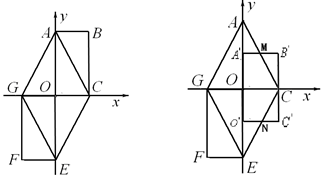
(1)请直接写出点F的坐标;
(2)试判断四边形ACEG的形状,并说明理由;
(3)将矩形OABC沿y轴向下平移m个单位(0<m<4),设平移过程中矩形与
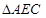 重叠部分面积为
重叠部分面积为 ,当
,当 :
: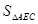 =11:16时,求m的值.
=11:16时,求m的值.(1)F(-2,-4);(2)四边形ACEG是菱形,证明见解析;(3)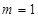 或
或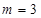 .
.
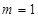 或
或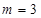 .
.试题分析:(1)点F与点B关于原点对称,故F(-2,-4);
(2)根据对角线互相垂直平分的四边形是平行四边形,即可证得;
(3)根据
 :
: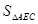 =11:16,求得
=11:16,求得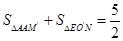 ,再由
,再由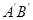 ∥
∥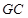 ,得到△
,得到△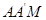 ∽△
∽△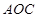 ,再用含m的代数式表示出
,再用含m的代数式表示出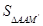 和
和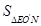 ,从而求出m的值.
,从而求出m的值.试题解析:(1)F(-2,-4);
(2)四边形ACEG是菱形.
理由:根据题意得:OA=OE,OC=OG
∴四边形ACEG是平行四边形
又∵AE⊥GC
∴四边形ACEG是菱形;
(3)将矩形OABC沿y轴向下平移m个单位得到矩形
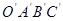 .设
.设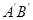 与AC交于点M,
与AC交于点M,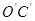 与EC交于点N,则当
与EC交于点N,则当 :
: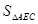 =11:16时,重叠部分为五边形
=11:16时,重叠部分为五边形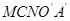 .
.∵
 :
: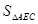 =11:16
=11:16∴
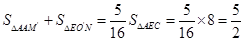
∵
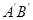 ∥
∥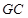 ,
,∴△
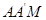 ∽△
∽△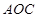
∴
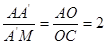
∴
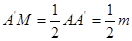
∴
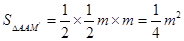
同理可得:
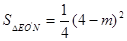
∴
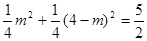
解得:
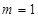 或
或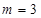 .
.
练习册系列答案
相关题目
 的三个顶点都在格点上(每个小方格的顶点叫格点).
的三个顶点都在格点上(每个小方格的顶点叫格点).


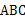 和△
和△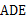 都是等腰直角三角形,∠
都是等腰直角三角形,∠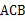 和∠
和∠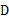 都是直角,点
都是直角,点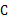 在
在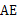 上,△
上,△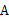 点经过逆时针旋转后能够与△
点经过逆时针旋转后能够与△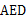 重合,再将图(1)作为“基本图形”绕着
重合,再将图(1)作为“基本图形”绕着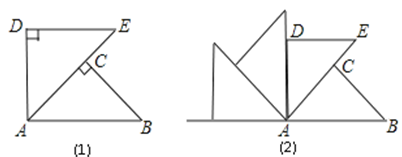

 后,得到的图案是( )
后,得到的图案是( )
